什么是时序预测

时序预测是给出某个历史一段时间中的变化情况，以预测未来一段时间内（或未来一个时刻）的变化情况。通常时序数据具有一定的趋势性和周期性，发现其中的规律，可以更好的预测未来将会发生的事情，做出更精确的决策。

目前时序预测可以在折线图和柱状图中使用，在 SaaS 高级版和多账号版本（非 2 账号版本）的私有部署中支持。

使用方式

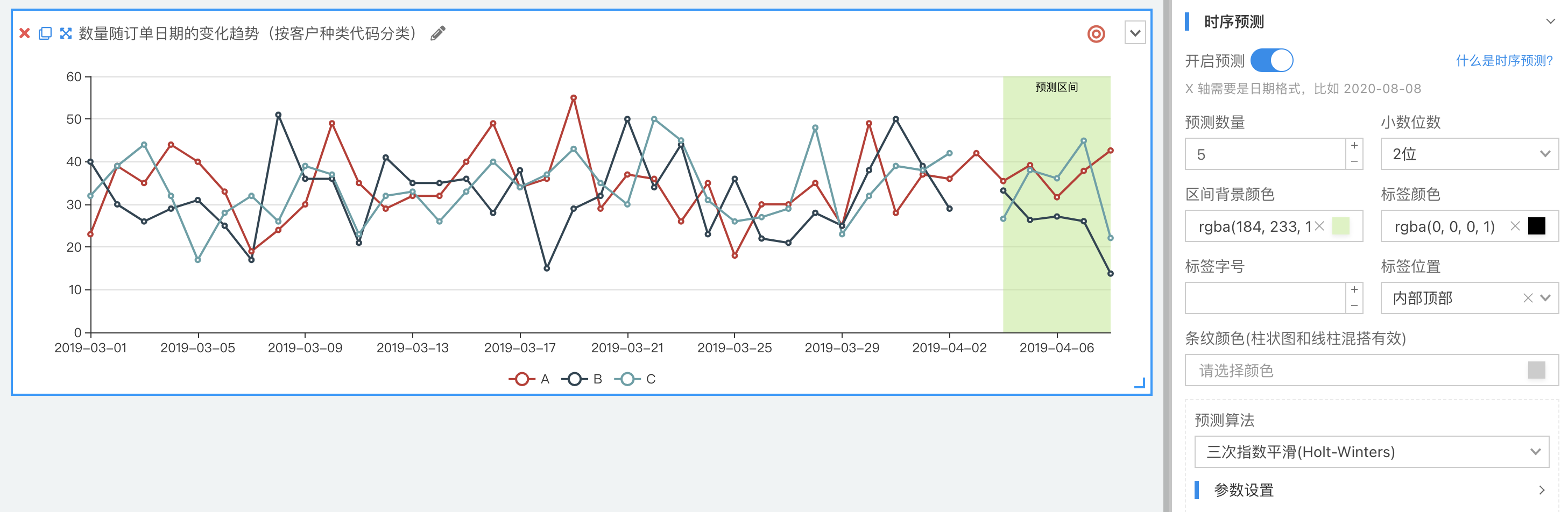
时序预测图表的 X 轴需要是日期格式，比如 2020-08-08。其他类型无法进行预测。 在折线图中，开启预测后就会对数据进行预测，预测结果会展示在预测区间内。可以设置预测区间相关的展示样式，例如，预测区间的颜色，标签信息等。默认会预测 5 天的数据，预测结果会保留 2 位小数位数。

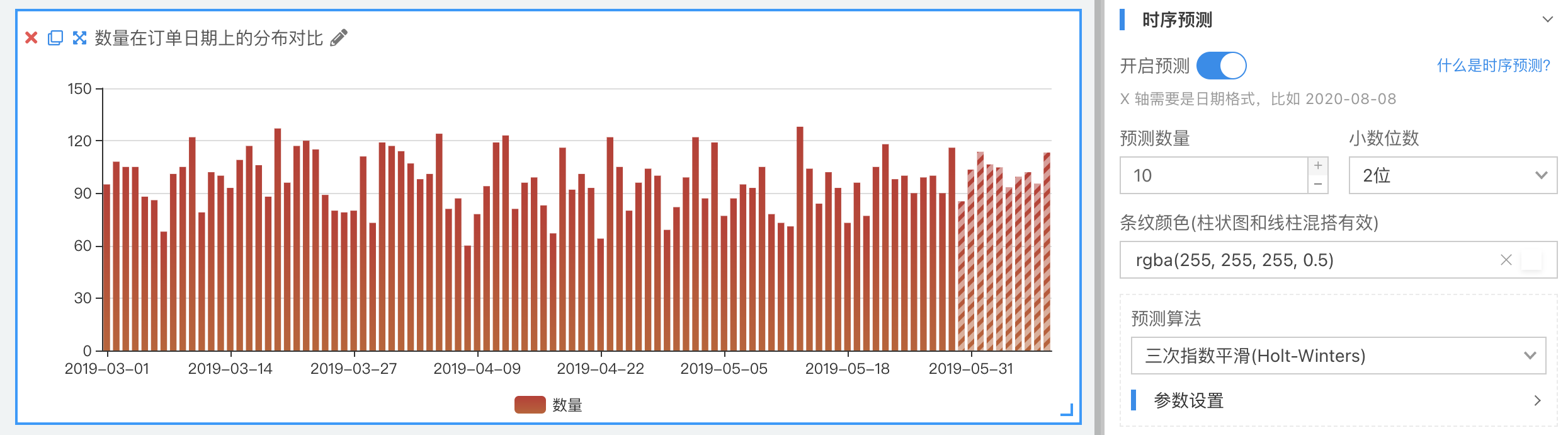
在柱状图中，预测数据使用的是带有条纹的柱子来进行展示的，可以设置条纹的颜色。

预测算法

可使用的时序预测算法包括两种，默认算法是三次指数平滑。

• 三次指数平滑(Holt-Winters)
• 季节性差分自回归移动平均(SARIMA)

Holt-Winters

三次指数平滑(Holt-Winters)包括三个平滑参数，它们的取值范围都为 [0, 1]。

• 水平平滑参数 α，默认值 0.5
• 趋势平滑参数 β，默认值 0.25
• 季节性平滑参数 γ。默认值 0.1

α 值是主观选定的，值越大表示对未来的预测中越近期的数据权重越大，因此也被称为记忆衰减因子，因为 α 的值越大，模型对历史数据“遗忘”的就越快。在市场预测中，α 的确定方法，一般是先根据经验做一个大概的预估，基本判断标准如下：

• 时间序列比较平稳时，选择较小的 α 值，0.05-0.20。
• 时间序列有波动，但长期趋势没大的变化，可选稍大的 α 值，0.10-0.40。
• 时间序列波动很大，长期趋势变化大有明显的上升或下降趋势时，宜选较大的 α 值，0.60-0.80。
• 当时间序列是上升或下降序列，α 取较大值，0.60-1。

较小的 γ 值意味着数据的周期性变化几乎没有，较小的 β 意味着数据的上涨或下跌的趋势几乎不会随时间变化。

具体的参数设置可以多试验几次以达到最佳效果。

SARIMA

季节性差分自回归滑动平均模型(Seasonal Auto Regressive Integrated Moving Average-SARIMA)包括六个参数。

• 自回归阶数 p，范围[0, 5]，默认为 2
• 差分阶数 d ，范围[0, 2]，0 为不差分，1 则是计算相邻观测值之间的差值，2 则意味着对原数据的“变化的变化”进行差分建模，默认值为 1
• 移动平均阶数 q，范围[0, 5]，默认为 2
• 季节性自回归阶数 P，范围[0, 3]，默认为 1
• 季节性差分阶数 D，范围[0, 1]，季节性差分是对一个观测值和相对应的前一周期的观测值之间进行差分，0 为不差分，1 为差分，默认值为 0
• 季节性移动平均阶数 Q，范围[0, 3]，默认为 1

当 P，D，Q 全都设置为 0 时，模型退化为差分自回归滑动平均模型(ARIMA)。在只有 p 不为 0 的时候，模型退化为自回归。在只有 q 不为 0，模型退化为移动平均模型。

具体的参数设置可以多试验几次以达到最佳效果。