特征工程

特征自动选择

使用特征选择方法，筛选出特征重要性前N的特征。如输入的特征数不足N时，则保留全部特征，目前支持三种特征选择方法：Gini增益、信息增益、信息值。

输入

• 输入一个数据集，选择需要筛选的特征列并设置挑选的特征数量与连续特征的分区数。

输出

• 输出筛选后的数据集与特征权值表。

算子参数

参数名称	是否必选	参数描述	默认值
特征选择方法	是	使用的特征选择方法；选择信息值时，标签列的唯一值数量必须为2，即二分类。	信息值
挑选TopN特征	是	根据特征重要性，保留TopN特征。如输入特征数不足TopN值，则保留全部特征 范围：[1, 2147483647]。	5
连续特征分区数	是	对连续特征进行分位数离散化的分区数 范围：[1, 2147483647]。	10

字段参数

参数名称	是否必选	参数描述	默认值
特征列	是	选择字段使用过滤法进行过滤，只能是数值或字符串类型。	无
标签列	是	标签列，标签列可以为字符串或整型。选择信息值时，标签列的唯一值数量必须为2，即二分类。	无

计算逻辑

• 使用特征选择方法，筛选出特征重要性前N的特征。如输入的特征数不足N时，则保留所有输入特征。
• 选择的特征列，只能是数值或字符串类型。
• 选择的数据标签列的值数量必须为2，即二分类。
• 对于连续特征可通过设置分区数可以进行离散化分箱操作。
• 当前支持的特征选择方法有：

使用示例

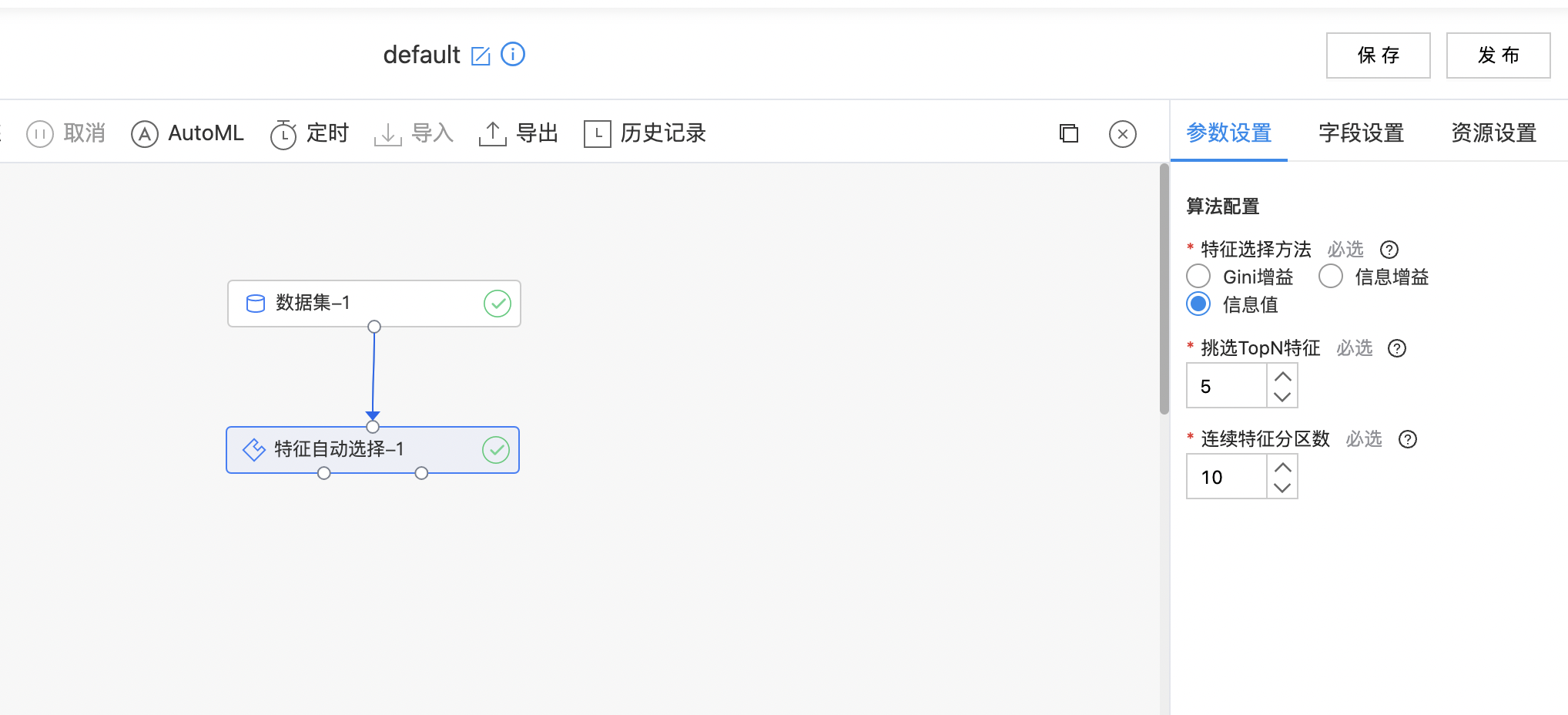
如下图所示，构建算子结构，配置特征选择方法。

特征自动衍生(spark)

依据数据集中的数值和字符串(枚举)类特征，自动衍生出大量新的特征，衍生方式包括数学运算衍生、笛卡尔积衍生和二值化衍生，衍生结果根据特征重要性排序，取 Top N 重要的衍生特征。

输入

• 输入是一个数据集，选择特征选择方法与数量，需要指定特征列（数值或字符串类型）和标签列（字符串或整型）。

输出

• 输出数据集和转化模型，其中数据集添加了指定数量的衍生特征。

算子参数

参数名称	是否必选	参数描述	默认值
特征选择方法	是	筛选衍生特征时使用的特征选择方法，支持Gini增益、信息增益。
衍生特征数	是	根据特征重要性，保留部分衍生特征 范围：[1, 2147483647]。
离散变量最大唯一值	是	以特征交叉的方式衍生离散变量时，允许的最大唯一值个数 范围：[16, 512]。	128

字段参数

参数名称	是否必选	参数描述	默认值
特征列	是	要进行衍生的特征列，只能是数值或字符串类型。	无
标签列	是	用来筛选衍生特征，标签列可以为字符串或整型。	无

计算逻辑

• 依据数据集中的数值和枚举类特征，自动衍生出大量新的特征。
• 将特征分为“数值”和“枚举”两大类，每一类两两成对组合进行特征衍生。
• 数值类做加减乘除的四则运算衍生，枚举类做特征交叉（笛卡尔积，可限制做笛卡尔积后的特征唯一值）。
• 将衍生得到的特征和原始的枚举特征一起，使用特征自动选择组件做重要性排序，取TopN重要的特征，并将这些特征中的枚举特征做onehot二值化处理。
• 当前支持的特征选择方法：Gini增益(GiniGain)、信息增益(InformationGain)，计算公式见特征自动选择组件。

使用示例

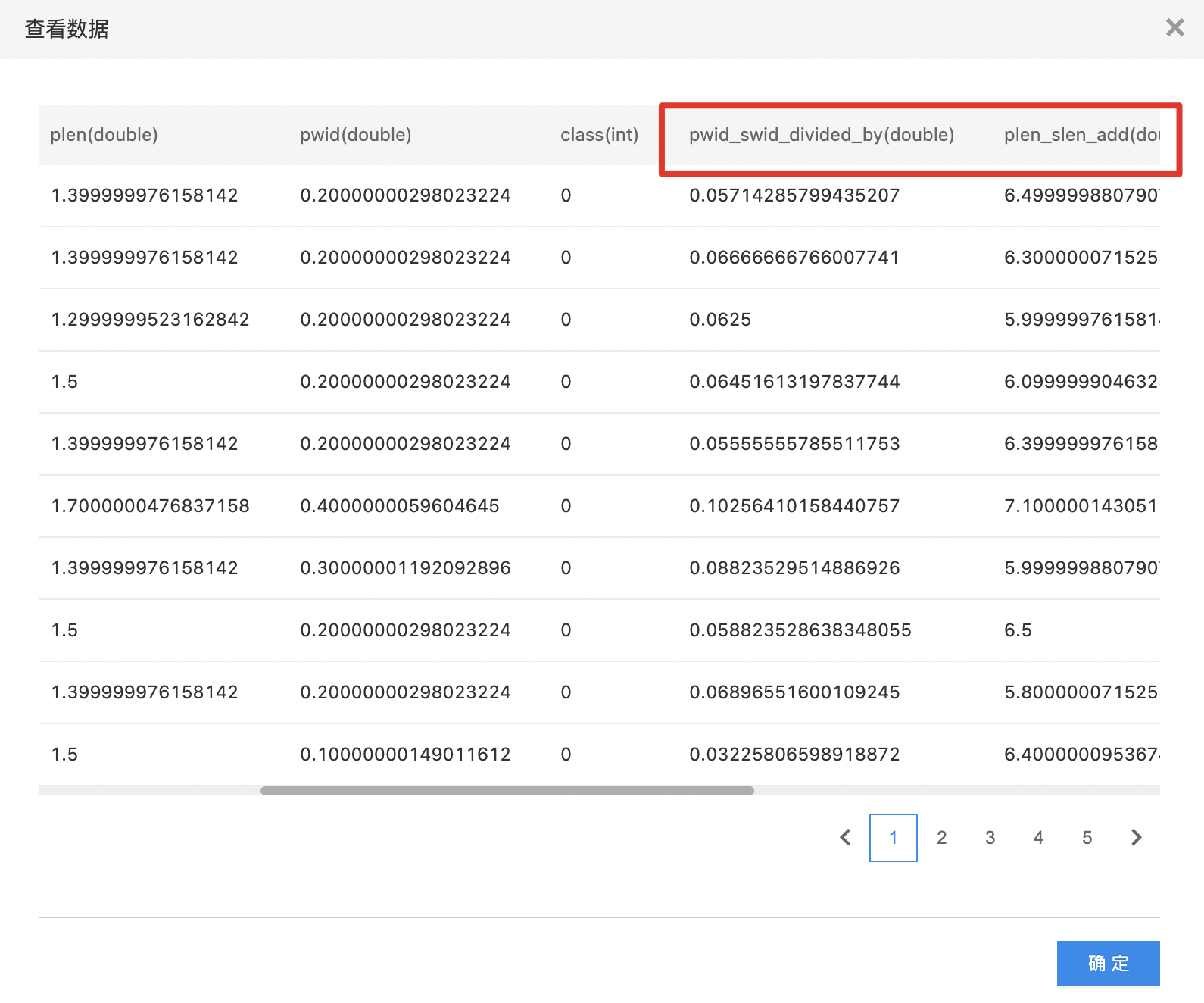
1. 如下图所示，构建算子结构，选择特征衍生的参考列，配置衍生方法。

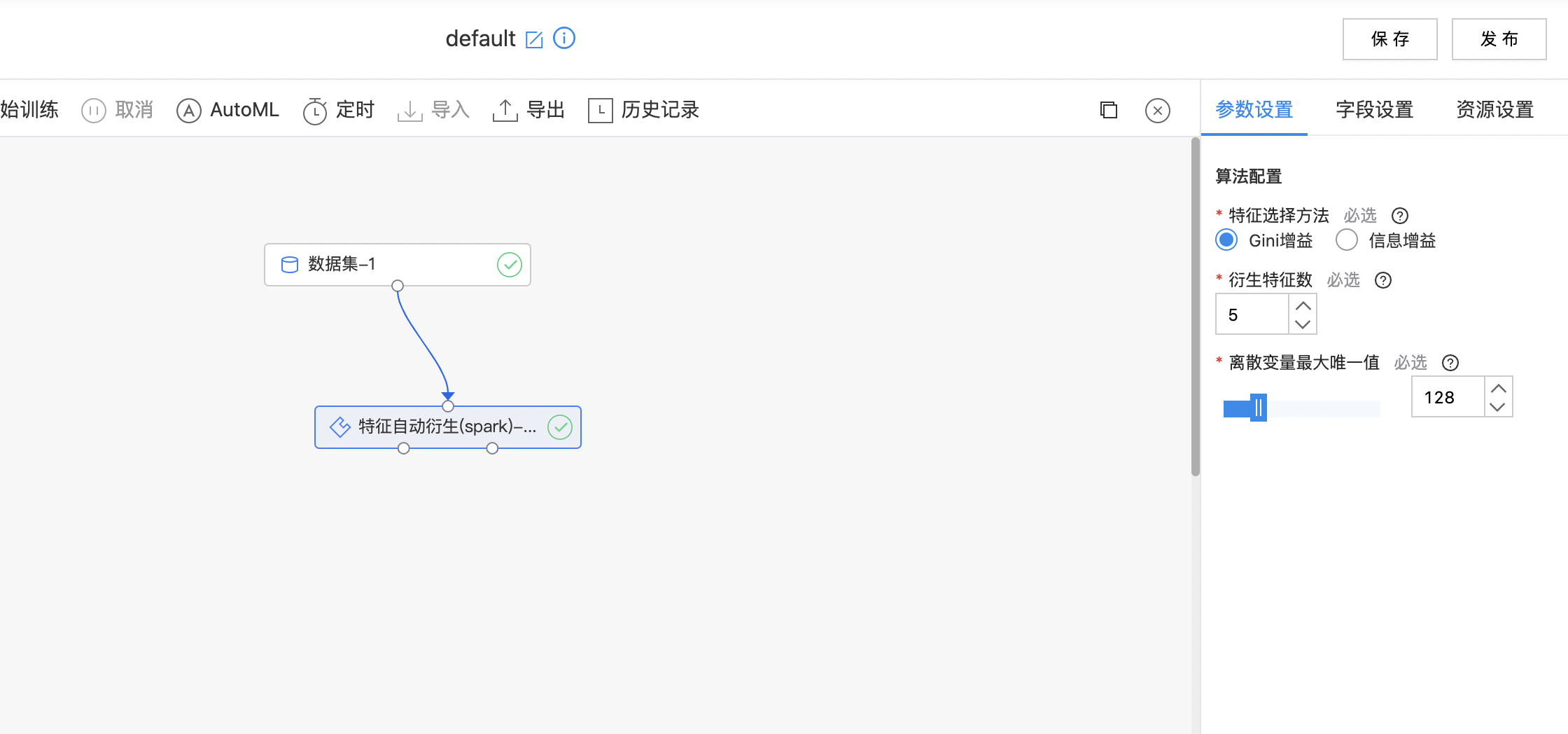
2. 查看特征衍生结果。

特征交叉

特征交叉需要选择至少两个特征列，通过笛卡尔积运算衍生新的特征列。

输入

• 输入是一个数据集，指定需要特征交叉的列集合。

输出

• 第一个输出是结果数据集。
• 第二个输出是特征交叉变换(Transformation)，后续可以使用这个变换操作其它数据集。

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	需要特征交叉的列集合，输入两列或三列非列表类型列	无

计算逻辑

• 选择表中的两列或三列非列表类型的列进行交叉。
• 多个特征做笛卡尔积：

在输入数据集的基础上添加了"featurecross_特征1_特征2..._特征n"一列，如“feature_cross_sex_age_work”，列的类型是String，内容是输入特征的笛卡尔积，如 "(男,24,工人)"。

使用示例

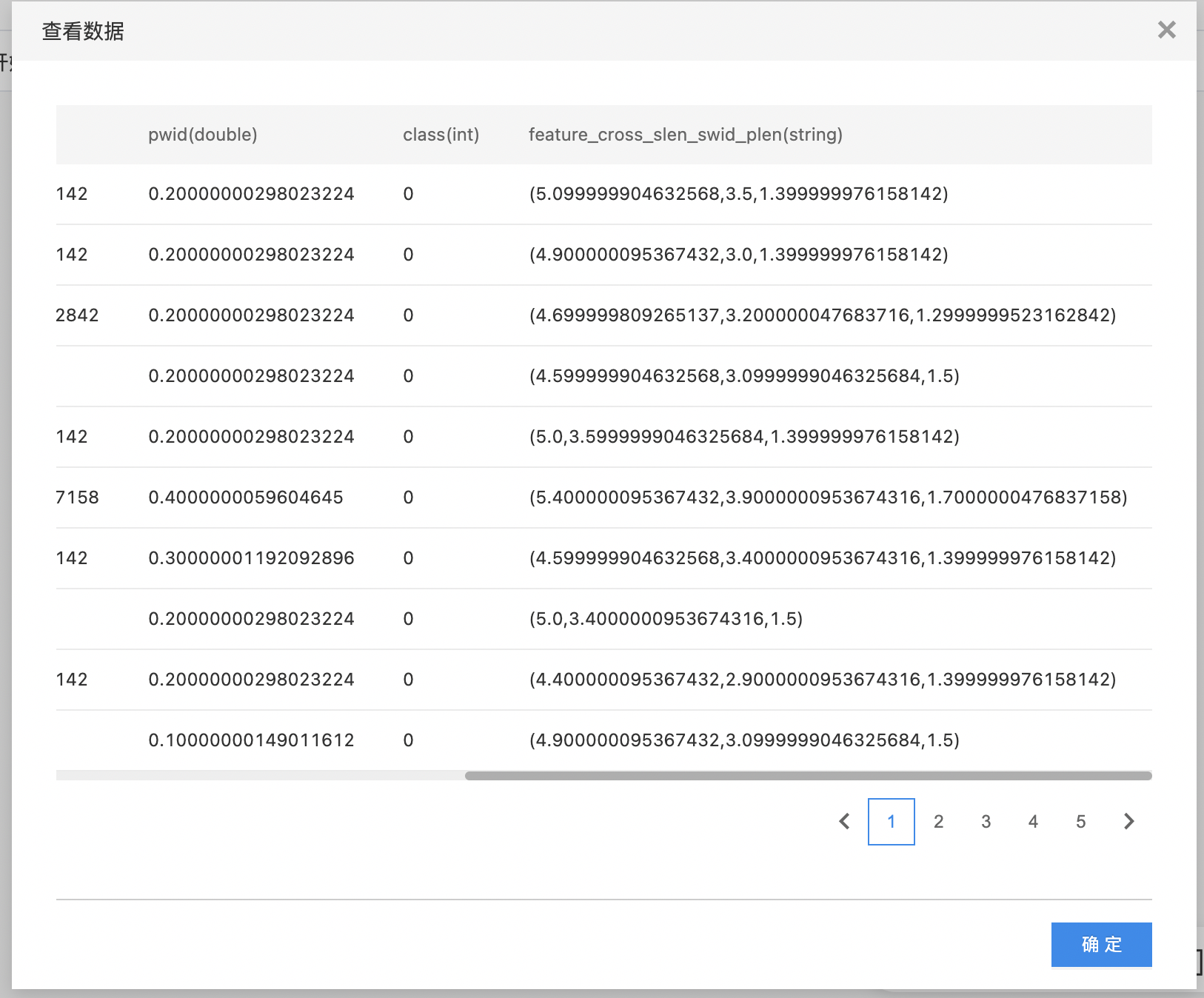
1. 如下图所示，构建算子结构，选择需要特征交叉的列。

2. 查看特征交叉结果。

多项式扩展

多项式扩展需要选择要做多项式扩展的列，至少选择2列，至多选择5列（防止衍生特征维度爆炸），选择的列的类型需要是数值类型，用户还可以选择是否保留原始列。

输入

• 一个数据集，指定需要做多项式扩展的列集合。

输出

• 第一个输出是结果数据集。
• 第二个输出是多项式扩展变换(Transformation)，后续可以使用这个变换操作其它数据集。

算子参数

参数名称	是否必选	参数描述	默认值
多项式次数	是	设置多项式次数，对于m个特征的n次多项式特征衍生，得到的特征个数与m的n次方是同阶的，为了防止衍生特征过多/维度爆炸，需控制多项式次数 范围：[2, 8]	2

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	需要多项式特征衍生的列集合，要求是数值类型；为了防止衍生特征过多，需控制输入列个数 范围：[2, 5]	无
保留原始列	是	是否保留原始列，保留后输出数据集包含原始数据列	开启

计算逻辑

• 多项式扩展是指在多项式空间中执行特征展开。
• 以一个二维特征向量（x，y）为例，将其进行二次多项式扩展，则扩展后的特征向量为（x, xx, y, xy, y*y）。
• 输出结果在输入数据集的基础上添加了"polyfeature原始列名(下划线分隔)"列，列的类型是vector,如果用户选择不保留原始列，输出数据集中会把原始列删掉。

使用示例

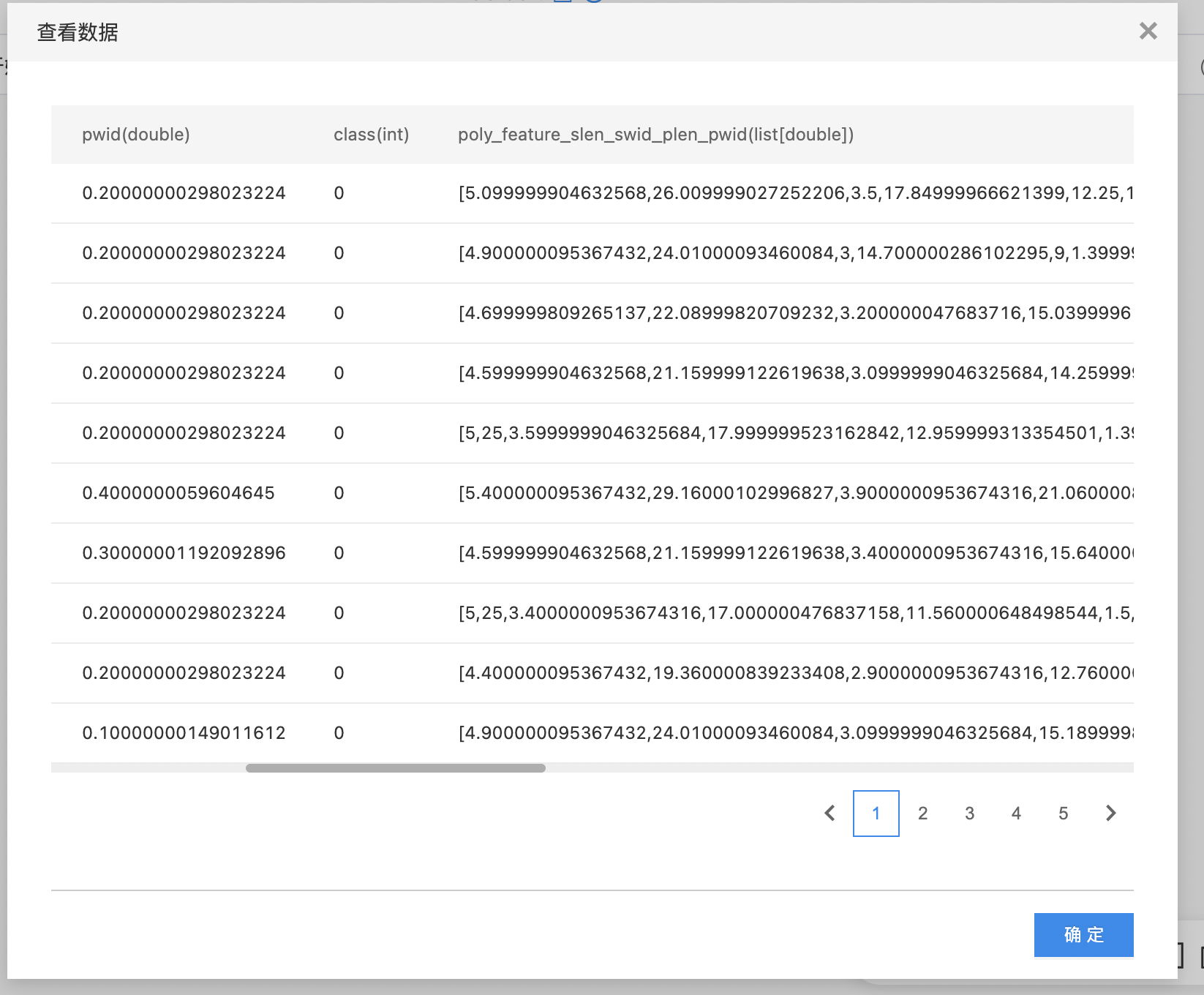
1. 如下图所示，构建算子结构，选择需要进行多项式扩展的列，配置扩展参数。

2. 查看多项式扩展结果。

时间戳特征衍生

时间戳特征衍生是指将时间戳或者日期类型特征列数据进行拆分处理，得到年、月、日等特征。

输入

• 输入是一个数据集，需要选择要做时间戳特征衍生的列，可以选择一列或多列，选择的列的类型需要是时间戳类型或日期类型。

输出

• 第一个输出是结果数据集。
• 第二个输出是时间戳特征衍生变换(Transformation), 后续可以使用这个变换操作其它数据集。

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	时间戳类型或日期类型列，可以输入多列	无

计算逻辑

• 时间戳特征衍生是指将时间戳或者日期类型特征列数据进行拆分处理，得到年、月、日等特征。

  • 衍生的特征

    • 时间戳类型：年、月、日、时、分、季度等等。
    • 日期类型：年、月、日、季度等等。

使用示例

1. 如下图所示，构建算子结构，选择需要特征衍生的时间戳列。

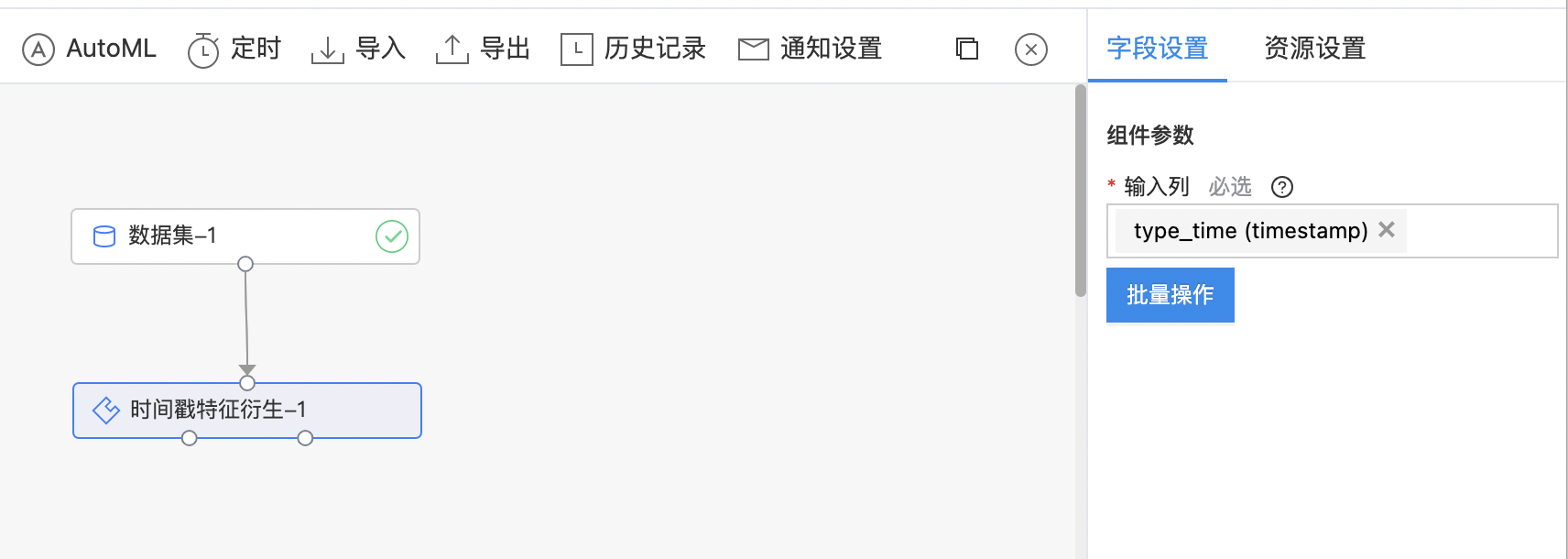
2. 查看时间戳衍生结果。

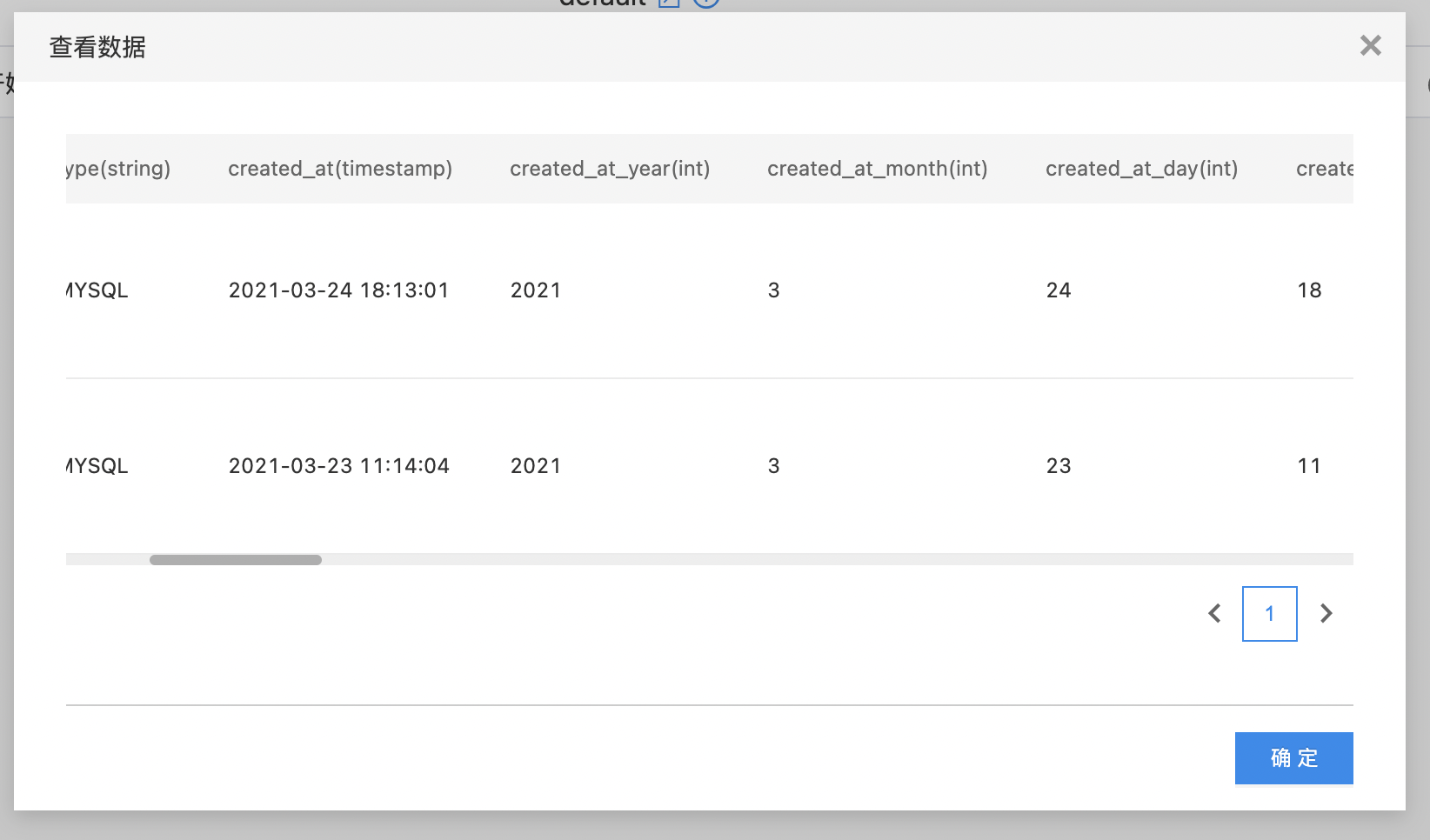
特征异常平滑

为了给数据集降噪，提升模型预测效果，特征异常平滑组件提供了三种特征平滑方式：Zscore平滑、百分位平滑、阈值平滑。

输入

• 输入一个数据集，选择要做平滑的列，选择的列需要是数值类型。

输出

• 第一个输出是结果数据集。
• 第二个输出是模型，连接特征工程预测组件进行预测。

算子参数

参数名称	是否必选	参数描述	默认值
特征异常平滑方式	是	特征异常平滑方式：Zscore平滑、百分位平滑、阈值平滑。	Zscore平滑
Zscore平滑方式中的阈值	是	设置阈值(theta)和数据计算出标准差(std)均值(mean)，将小于(-theta*std+mean)的值替换为(-theta*std+mean)和将大于(theta*std+mean)的值替换为(theta*std+mean)范围：[1.0, inf)。	3
最小百分位数位置	是	最小百分位数的位置，将小于最小百分位数的值替换为最小百分位数，最小百分位数的位置应小于等于最大百分位数的位置，如设置为50则表示为中位数，假设p为最小百分位数的位置对应的值为pv，则将小于pv的值设置为pv 范围：[0.0, 100.0]	0
最大百分位数位置	是	最大百分位数的位置，将大于最大百分位数的值替换为最大百分位数，最大百分位数的位置应大于等于最小百分位数的位置，如设置为50则表示为中位数，假设p为最大百分位数的位置对应的值为pv，则将大于pv的值设置为pv 范围：[0.0, 100.0]	100
最小阈值	是	将小于最小阈值的值替换为最小阈值，最小阈值应大约等于最大阈值。	-10000
最大阈值	是	将大于最大阈值的值替换为最大阈值，最大阈值应大于等于最小阈值。	10000
保留原始列	是	是否保留原始列。	开启

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	选择字段进行特征异常平滑，需要是数值类型。	无

计算逻辑

• 特征异常平滑是指对输入的特征使用异常判断方式，对判断为异常的数据进行处理。

• 当前实现的异常平滑方式有ZScore平滑、阈值平滑和百分位平滑:

  • ZScore平滑：利用设置的阈值(theta)和数据计算出的标准差(std)均值(mean)，将小于(-thetastd+mean)的值替换为(-thetastd+mean)和将大于(thetastd+mean)的值替换为(thetastd+mean)。
  • 阈值平滑：利用设置的最小阈值和最大阈值，将小于最小阈值的值替换为最小阈值，将大于最大阈值的值替换为最大阈值。
  • 百分位平滑：利用设置的最小百分位和最大百分位，将小于最小百分位数的值替换为最小百分位数，将大于最大百分位数的值替换为最大百分位数。

使用示例

1. 如下图所示，构建算子结构，选择需要特征异常平滑的列，配置平滑方式。

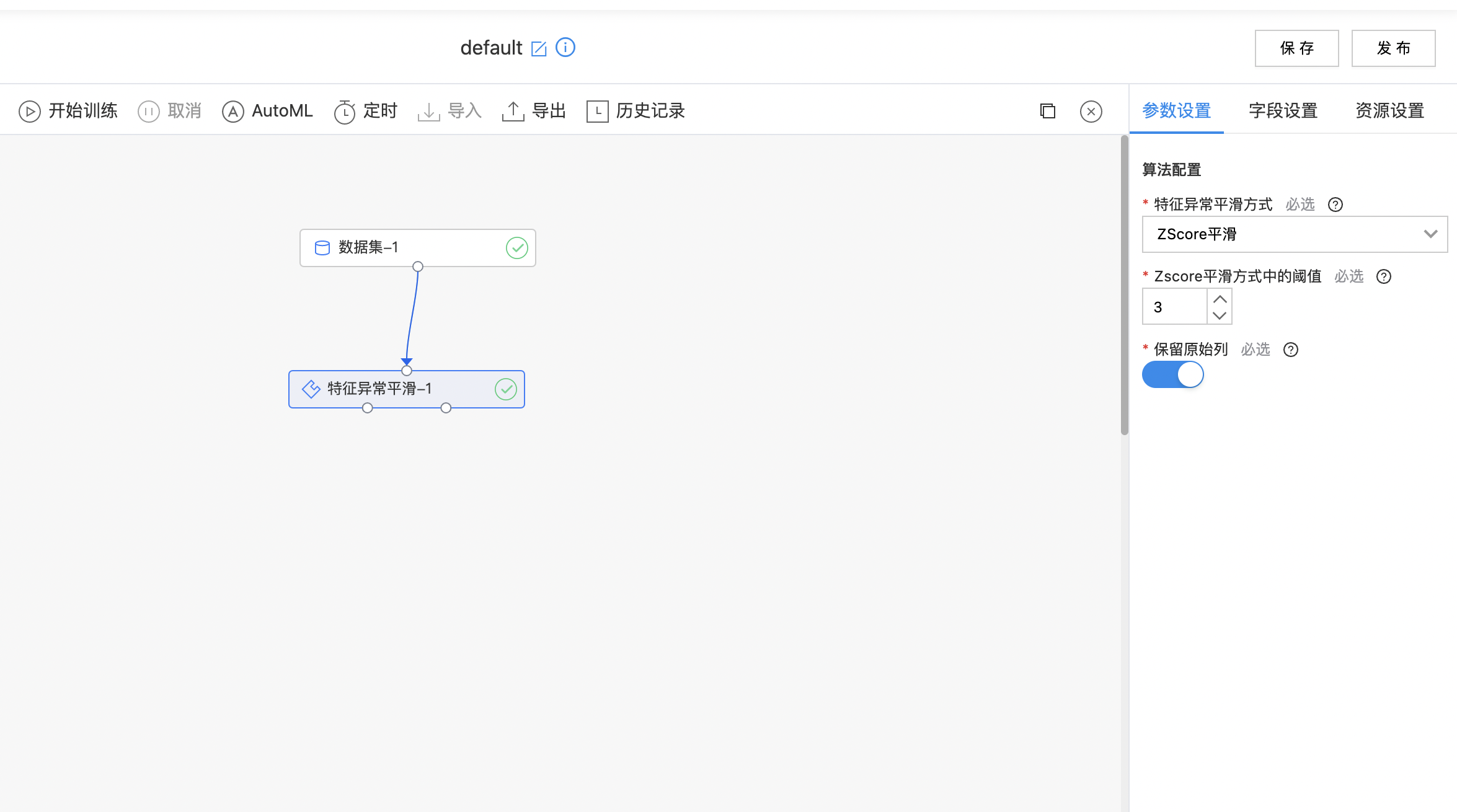
2. 查看特征异常平滑结果。

分箱

分箱组件可选择多列指定统一的规则对Double,Vector,Integer,String进行分箱，目前支持等频、等宽和自定义区间三种分箱方法。

输入

• 输入一个数据集，选择分箱方式与对应的分箱策略。

输出

• 第一个输出为结果数据集。
• 第二个输出是模型，连接特征工程预测组件进行预测。

算子参数

标签列	是	分箱的依据	无
参数名称	是否必选	参数描述	默认值
分箱方式	是	分箱方式，目前自定义区间仅对数值型列有效。不同分箱方式对数值类型列分箱方式不同；对字符串类型列分箱方式相同，都是将字符串映射成数字 参数可选值:  EQUALWIDTH : 等宽分箱  DECISIONTREE : 决策树分箱  CUSTOMEDGES : 自定义区间  QUANTILES : 等频分位数分箱  CHIMERGE : 卡方分箱	等频分位数分箱
分箱个数	是	指定输入列连续特征的默认分箱个数 范围：[2, inf)。	10
自定义分箱区间	是	连续特征自定义分箱区间，每条区间以英文分号隔开。每列的区间类似[col:]-inf,2.0,3.0,inf指定。第一条自定义区间为对所有选定列的默认规则。vector以(列名_i)表示vector的第i列	无
决策树最大深度	是	指定输入列连续特征的决策树模型最大深度，假设最大深度为k，那么对应的最大分箱数为pow(2,k) 范围：[1, inf)	5
自定义分箱个数	否	自定义分箱个数，对具体某一列的分箱个数进行指定。以英文分号间隔，每条规则以":"间隔，例如a:3;b:10。	无
是否保存原始列	是	是否保存原始列，为true时，处理过的列重命名 "bin_"前缀	关闭

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	分箱列，可以是数值、字符串或数值数组类型；依据标签列分箱方法：卡方分箱要求标签列是数值类型，决策树分箱要求标签列是字符串或数值类型	无

计算逻辑

对表中的列，进行分箱处理，将数据映射到对应的箱中，所选的列应是数值、字符串或数值数组类型

等宽分箱:

• 指定默认分箱个数后，按照列中的最小值到最大值之间，将数据N等分，数据分到每个箱中，和等频分箱相比每个箱中的数据量不固定。
• 自定义分箱个数，对具体某一列的分箱个数进行指定。以;间隔，每条规则以:间隔，例如a:3;b:10。

决策树分箱：

• 决策树分箱是一种自上而下的分箱方法，通过计算信息增益，我们可以对单个自变量的划分生成决策树。决策树的分裂节点就是每个箱的边界。最终得到的叶子节点就是每一个箱。

自定义区间

• 自定义区间分箱，目前仅对数据值列有效
• 连续特征自定义分箱区间，每条区间以;隔开。每列的区间类似[col:]-inf,2.0,3.0,inf指定。第一条自定义区间为对所有选定列的默认规则。例子1.0,2.0;a_1:3.0, 4.0即定义了[1.0,2.0]和[3.0,4.0]两个分箱区间

等频分位数分箱:

• 指定默认分箱个数后，将数据分箱到每个箱中并且每个箱中的数据量大致相等
• 自定义分箱个数，对具体某一列的分箱个数进行指定。以;间隔，每条规则以:间隔，例如a:3;b:10

卡方分箱：

• 卡方分箱是一种自底向上的(即基于合并的)数据离散化方法。 先算出单变量每个取值的卡方值，再把卡方值相近的取值合并到一个箱里。

使用示例

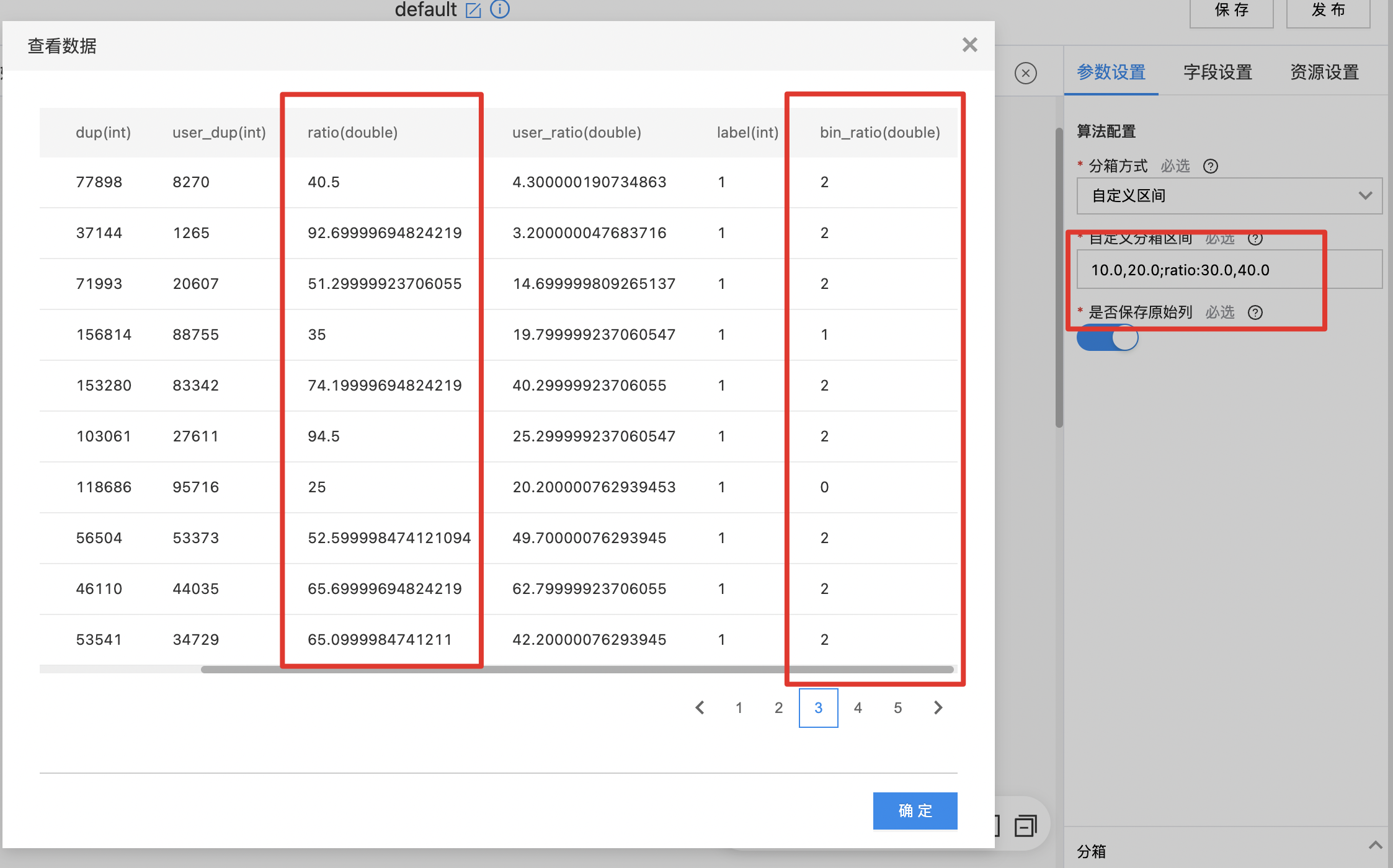
1. 拖入数据集组件：

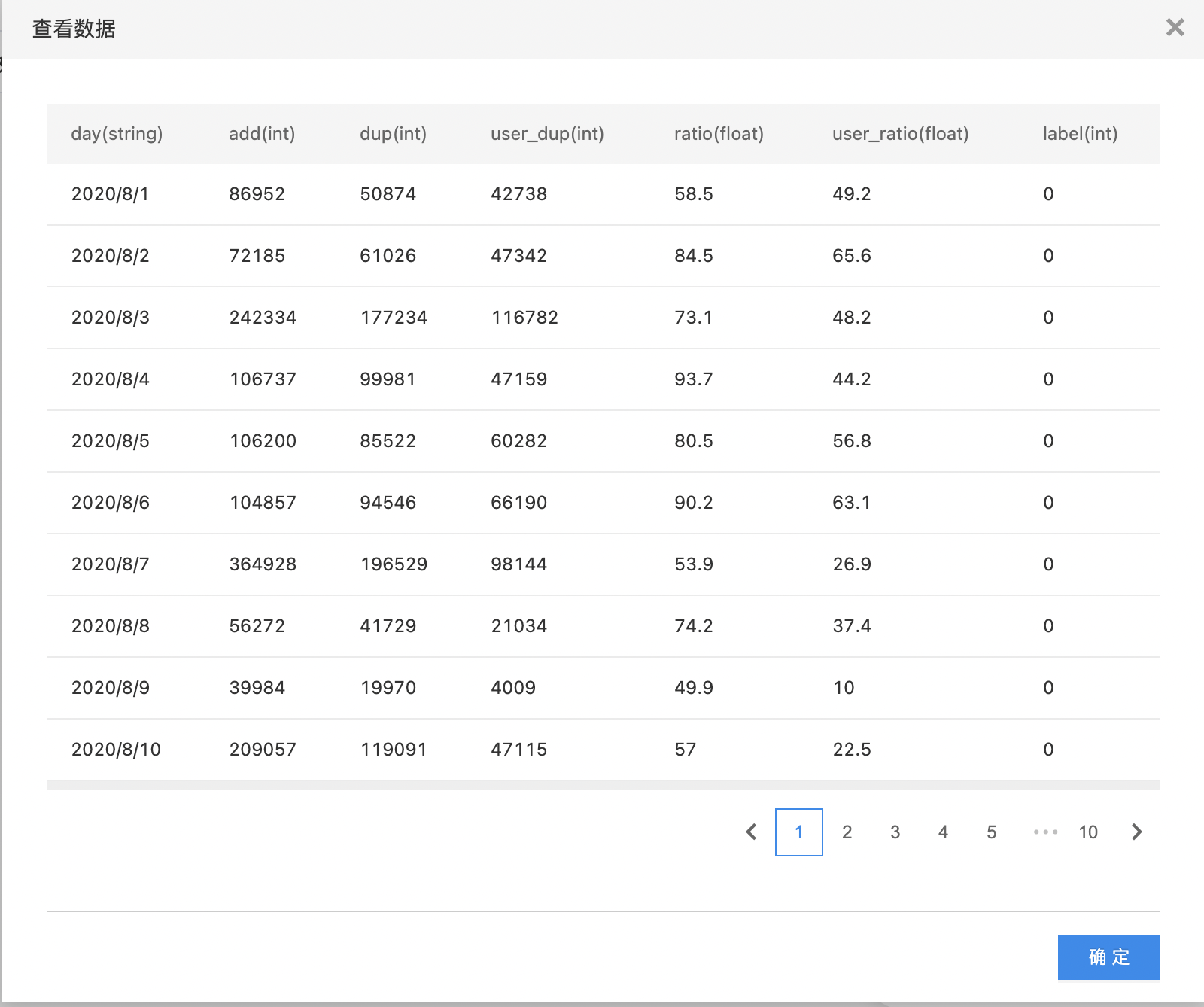
2. 设置自定义分箱区间，该示例针对ratio列进行分箱，可以从图例中看出分为了0，1，2三个分箱。

特征哈希

特征哈希将一组分类或数值特征投影到指定维度的特征向量中（通常比原始特征空间维度小得多），在特征维度过大的时候，容易产生特征稀疏的现象，导致模型收敛速度过慢、模型参数爆炸等问题，特征哈希用低维度向量表示高维度特征可以有效的缓解上述问题。

输入

• 输入一个数据集，需要选择要做特征哈希的列。输入列的类型需要是数值、字符串或布尔类型。
• 可以设置要视为分类特征的数值列（可选），用户还可以选择是否保留原始列。

输出

• 第一个输出是结果数据集，在输入数据集的基础上添加了"featurehash原始列名(下划线分隔)"列，列的类型是spark vector。如果用户选择不保留原始列，输出数据集中会把原始列删掉。
• 第二个输出是特征哈希变换（Transformation），后续可以使用这个变换操作其它数据集。

算子参数

参数名称	是否必选	参数描述	默认值
输出向量维度	是	特征数量。应该大于0（默认值=262144）。由于是使用哈希值的简单模来确定向量索引，因此建议设置此参数的值为2的幂；否则，这些特征将不会均匀地映射到向量索引。 范围：[1, inf)	262144

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	需要特征哈希的列集合，要求不是数组类型。	无
要视为分类特征的数值列	否	默认情况下，只有字符串列和布尔列被视为分类特征，可以使用此参数显式指定要视为分类特征的数值列。注意，相关列也必须在＇输入列＇中设置。	无
保留原始列	是	是否保留原始列。	关闭

使用示例

1. 如下图所示，构建算子结构，选择需要进行特征哈希的列，配置输出向量维度。

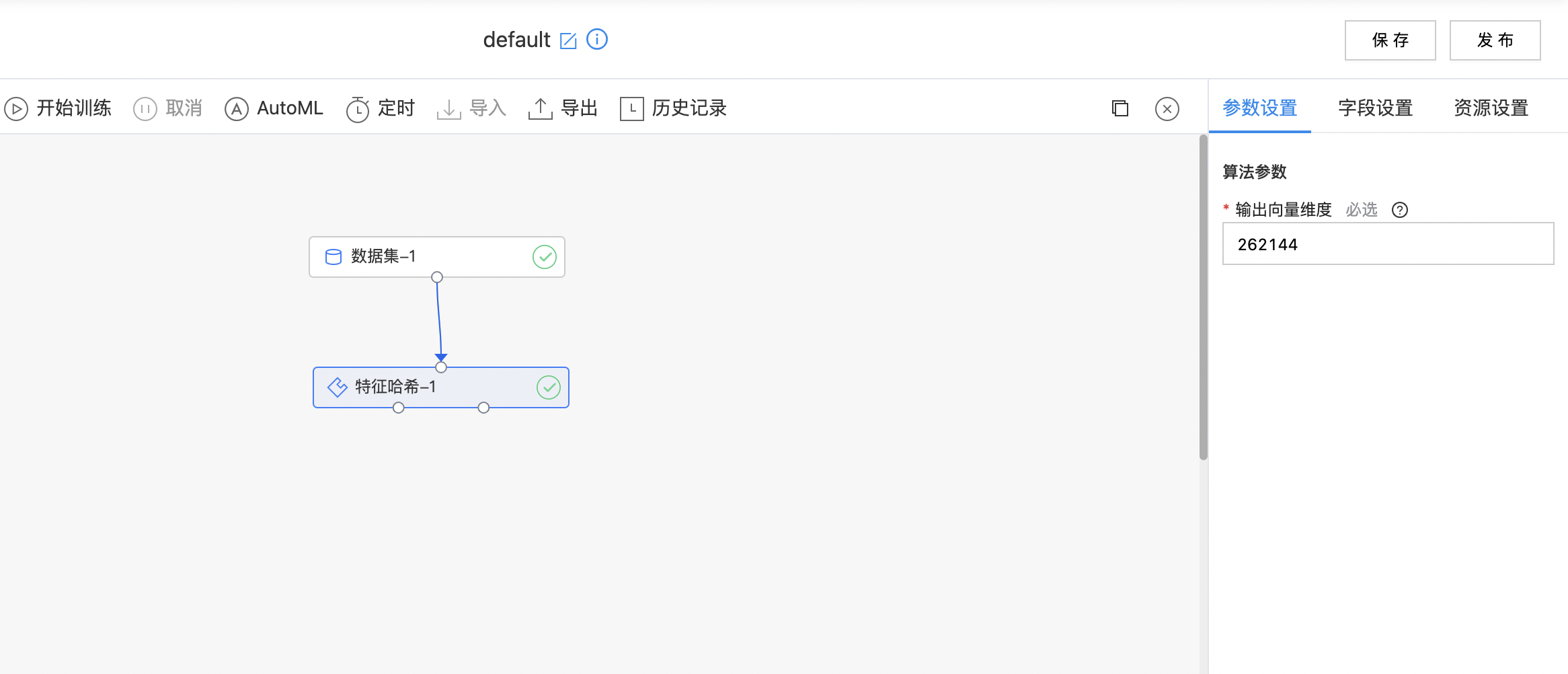
2. 查看特征哈希结果。

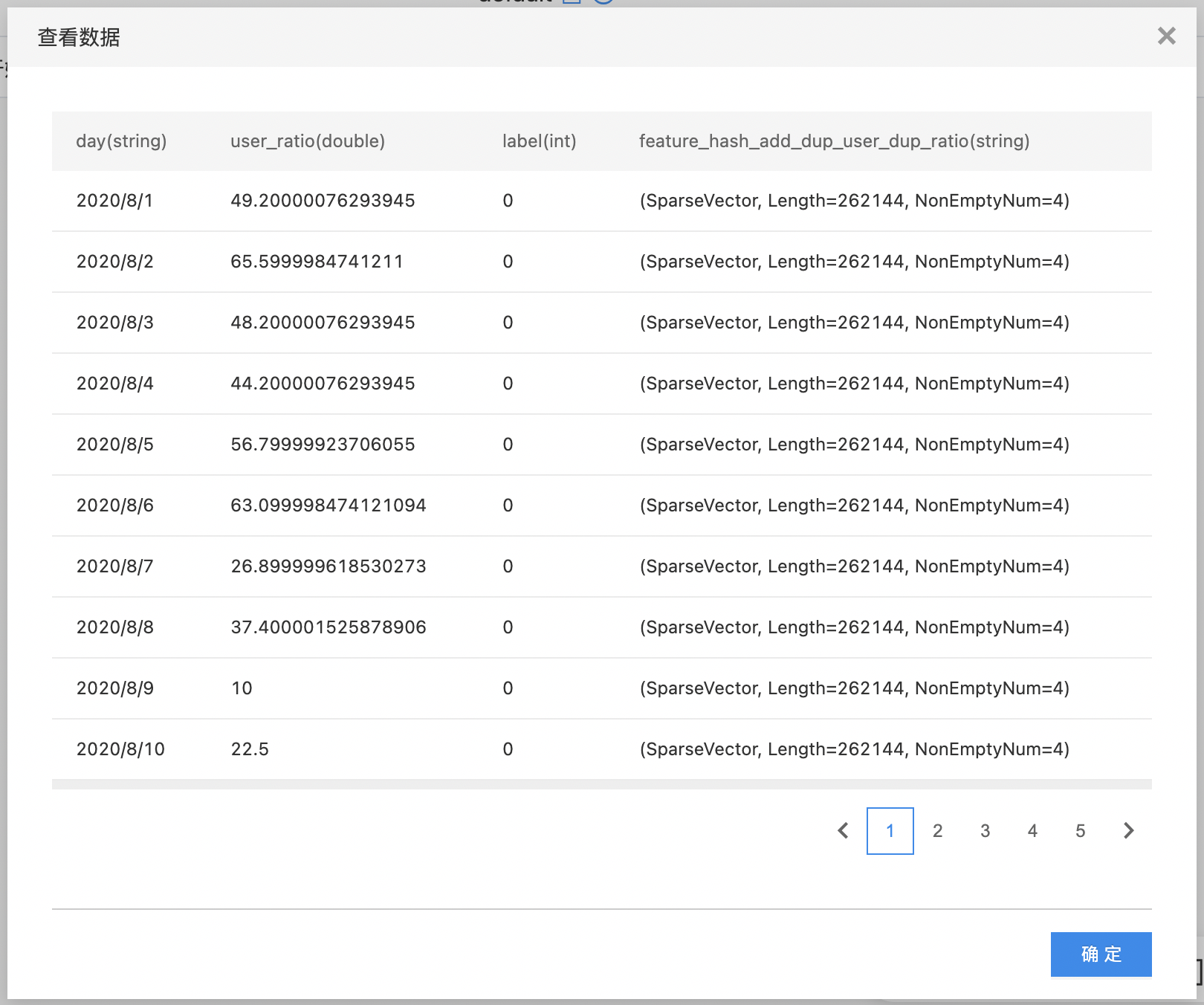
OneHot(哑编码)

OneHot(哑编码)支持独热码和哑编码两种编码方式，两种编码方式都是为了帮助模型更好的处理属性数据问题，在一定程度上也起到扩充特征的作用。独热码从n个变量推论出所有类别，特征数据直观但存在特征冗余的情况；相对于独热码，哑编码从n-1个变量推论出n个类别，数据不够直观但不冗余，通常线性模型有截距项的时候推荐使用哑编码的方式处理特殊。

输入

• 输入一个数据集，需要选择要做onehot的列，可以选择一列或多列；选择的列的类型需要是String或数值类型，用户还可以选择是否保留原始列。

输出

• 第一个输出是结果数据集，在输入数据集的基础上添加了"onehot_原始列名"列，列的类型是Vector，内容是onehot的SparseVector。如果用户选择不保留原始列，输出数据集中会把原始列删掉。
• 第二个输出是Onehot变换（Transformation），后续可以使用这个变换操作其它数据集。

算子参数

参数名称	是否必选	参数描述	默认值
编码方式	是	哑编码会将训练集中未出现的类以零向量表示；独热编码会将每一类编码成一个特征维度。	哑编码

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	需要onehot的列集合，要求不是数组类型	无
保留原始列	是	是否保留原始列	关闭

计算逻辑

假设当前有一个数据集(人口学历统计)，其中四个样本示例如下：

姓名	学历
小明	小学
小红	初中
小刚	高中
小亮	大学

使用独热码结果如下：

姓名	小学	初中	高中	大学
小明	1	0	0	0
小红	0	1	0	0
小刚	0	0	1	0
小亮	0	0	0	1

使用哑编码结果如下：

姓名	小学	初中	高中
小明	1	0	0
小红	0	1	0
小刚	0	0	1
小亮	0	0	0

根据小亮与小明、小红、小刚三人的特征值不同可以推断出小亮的学历为大学。

使用示例

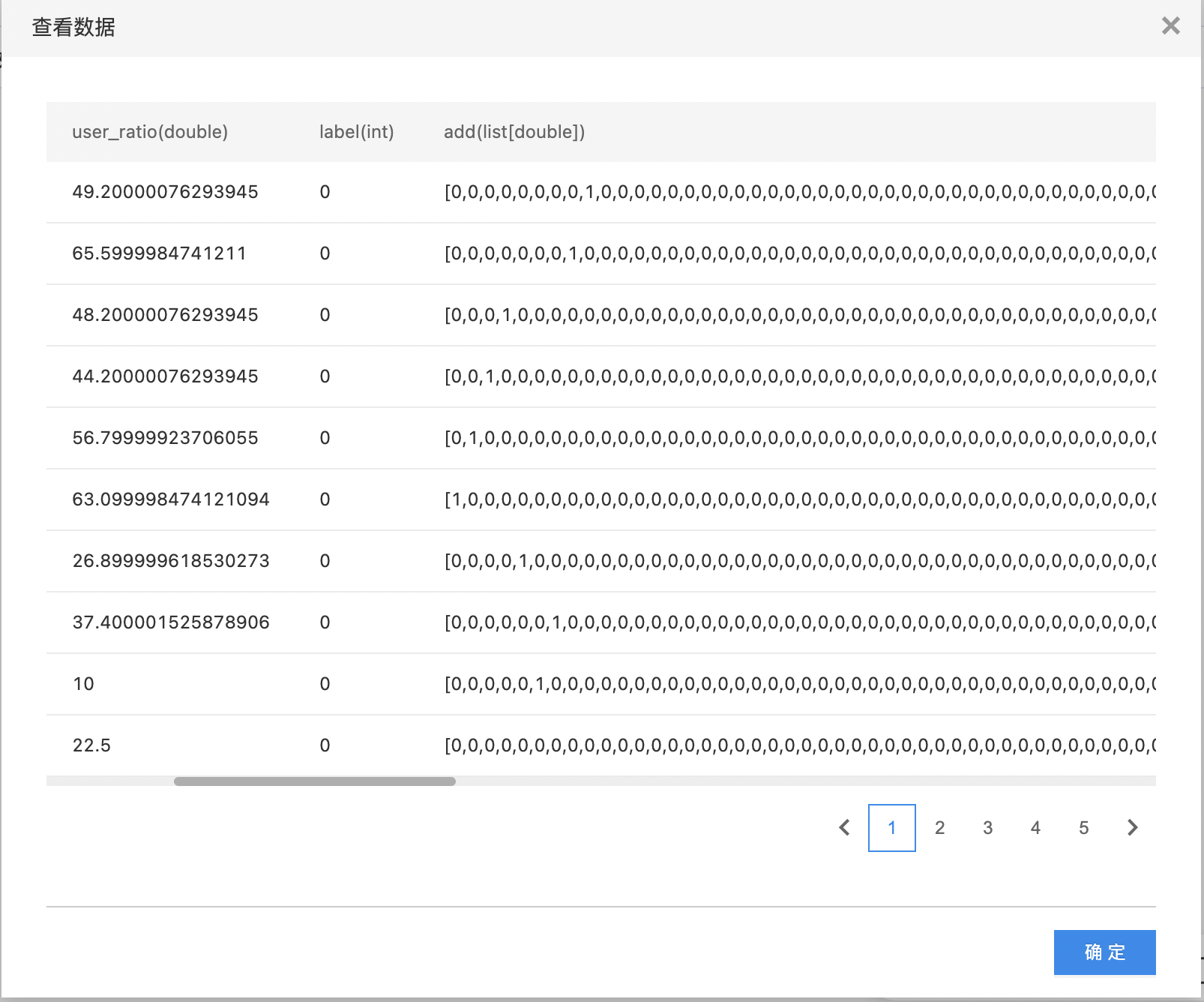
1. 如下图所示，构建算子结构，选择需要OneHot编码的列，选择编码方式。

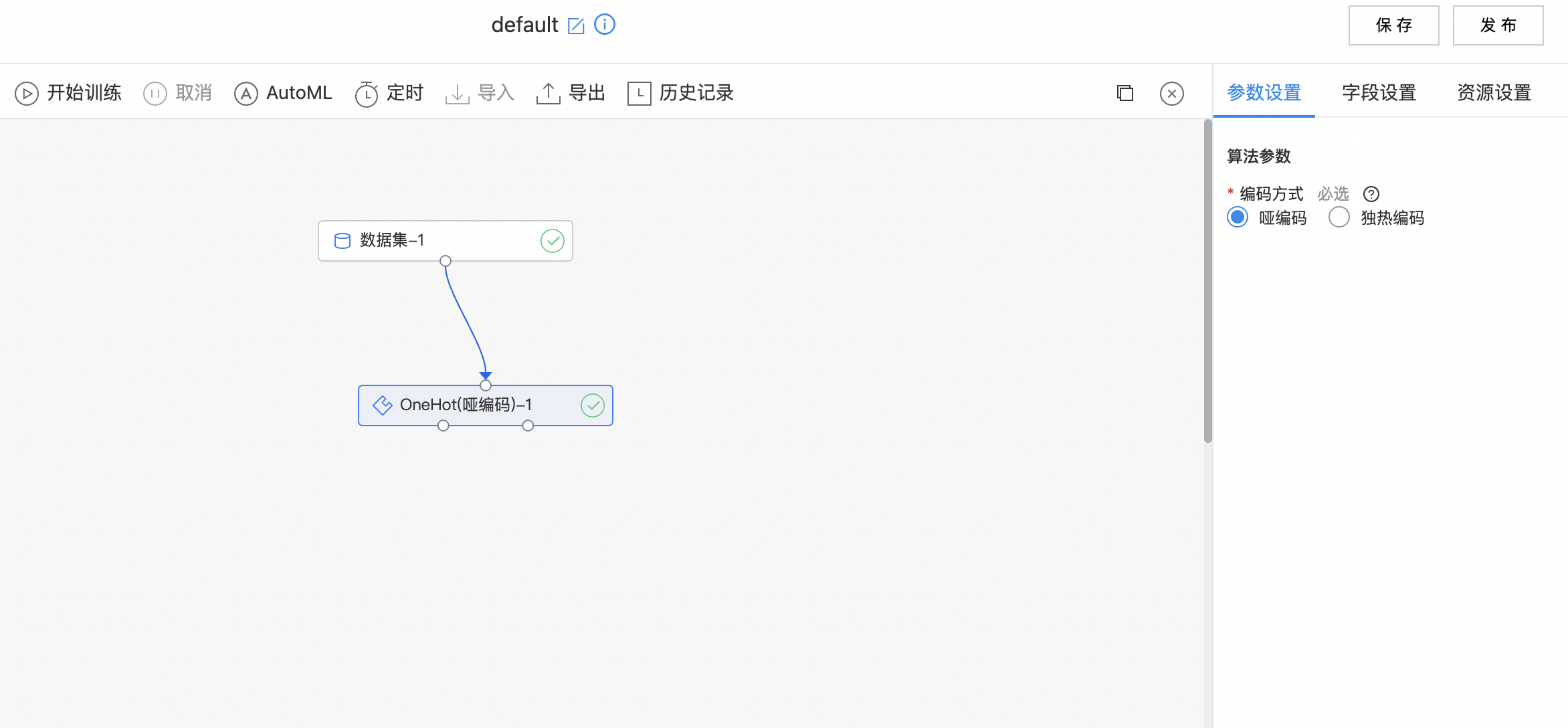
2. 查看OneHot编码结果。

异常值处理

异常值处理组件选择列处理,需与选择的填充规则匹配其中浮点型或数值数组型支持NULL,NAN,NULLORNAN,CUSTOMVALUE;整型支持NULL,CUSTOMVALUE；字符串型支持NULL,NULLOREMPTY,CUSTOMVALUE。

输入

• 输入一个数据表，用户可选择多列指定统一的规则对异常值进行处理，也可以按格式输入多行自定义规则，但列名不允许重复。

输出

• 第一个输出为结果数据集。
• 第二个输出是模型，连接特征工程预测组件进行预测。

算子参数

参数名称	是否必选	参数描述	默认值
异常值类型	是	异常值类型： CUSTOMVALUE(String和数值型) EMPTY(String) NAN(double,数值数组型) NULL(数值型,数值数组型和String) NULLOREMPTY(String) NULLORNAN(double,数值数组型)	NULL(数值型,数值数组型和String)
自定义异常值	是	自定义异常值,仅支持String和数值型	无
填充类型	是	使用的填充类型： CUSTOMVALUE(String和数值型) MAX(数值型和数值数组型) MEAN(均值，数值型和数值数组型) MEDIAN(中位数,数值型) MIN(数值型和数值数组型) MODE(众数,String和数值型) QUANTILE(数值型) RANDOM(数值型)	MIN(数值型和数值数组型)
自定义异常值处理规则	否	自定义异常值处理规则,输入的列名与输入列不能重复。以英文分号间隔，每条规则含5列以","间隔,包含col(列名),outlierType(异常值类型),customOutlier(自定义异常值),fillerMethod(填充类型),customFillValue(自定义填充值)。	无

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	选择字段进行异常值处理,需与选择的填充规则匹配。浮点型或数值数组型支持NULL,NAN,NULLORNAN,CUSTOMVALUE；整型支持NULL,CUSTOMVALUE；字符串型支持NULL,NULLOREMPTY,CUSTOMVALUE	无

使用示例

1. 拖入数据集组件，本示例以自定义处理label列为样例：

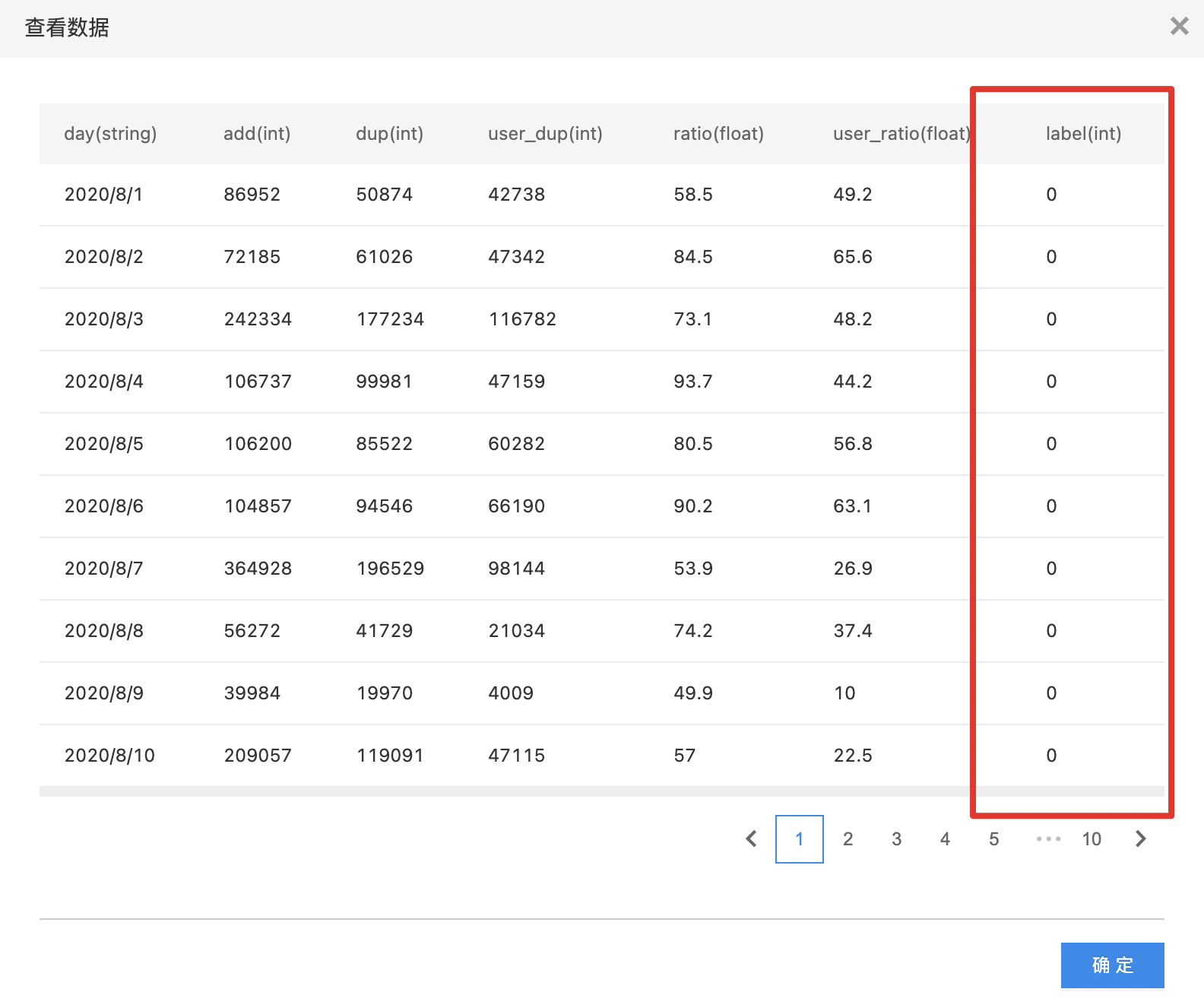
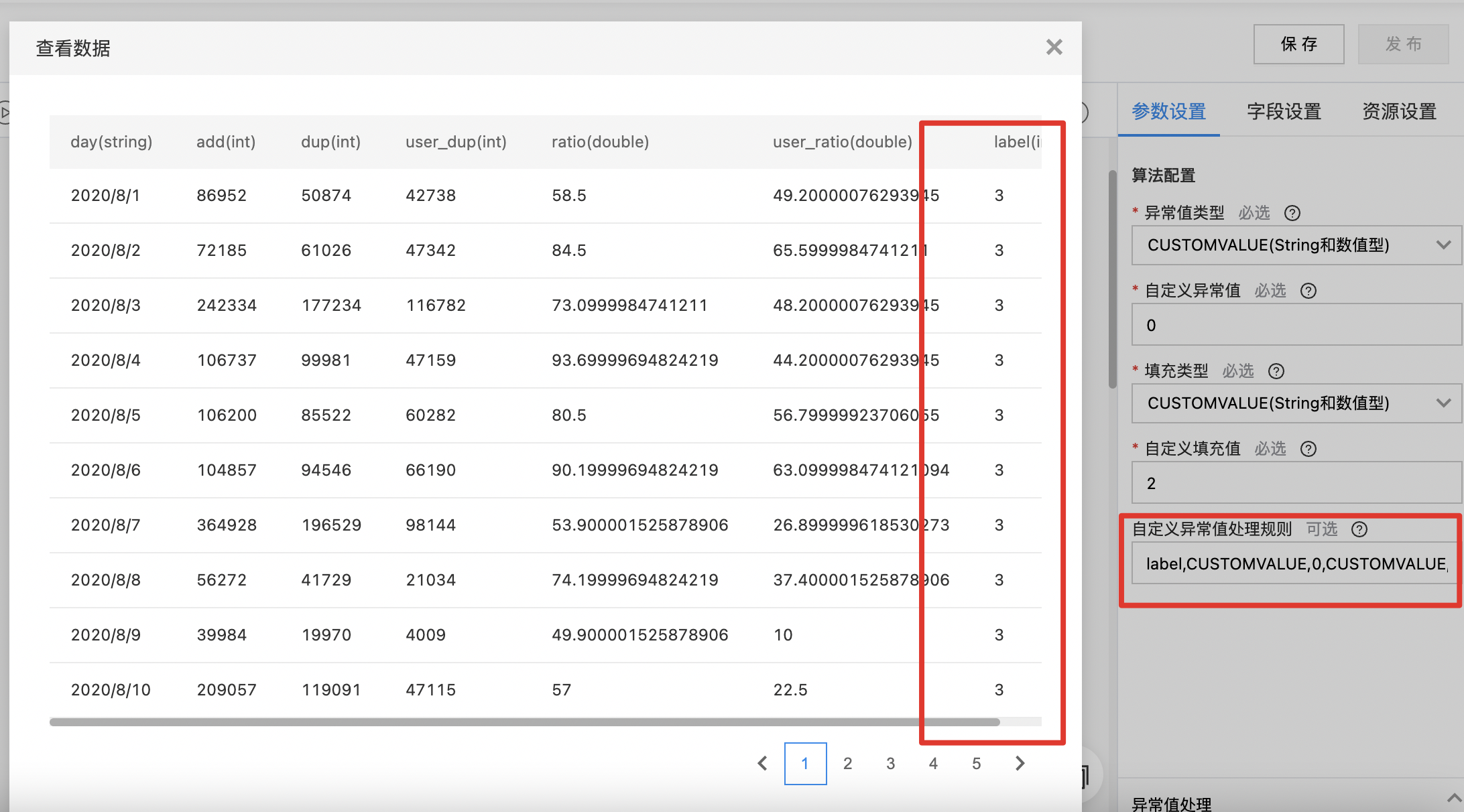
2. 输入自定义规则参数：label(列名),CUSTOMVALUE(异常值类型),0(自定义异常值),CUSTOMVALUE(填充类型),3(自定义填充值);

从图例中可知，自定义异常值0已经被替换为3。

PCA主成分分析

PCA主成分分析法是一种常用的一种降维手段，它主要是基于方差来提取最有价值的信息。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量。

输入

• 输入一个数据集，用户选择要做PCA的列（必须是int或double或vector类型），输入PCA结果的列数，并且可以选择PCA之前是否中心化、标准化，可以选择是否保留原始列。

输出

• 第一个输出是这个数据集的pca结果。
• 第二个输出是可以对其它数据集应用的PCA模型。

算子参数

参数名称	是否必选	参数描述	默认值
结果维度	是	PCA结果的维度 范围：[1, inf)	无
预处理方式	是	主成分分析前的预处理，"中心化"指将每个特征的均值调整成0，"标准化"在中心化的基础上将每个特征的标准差化成1	无

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	需要PCA的列集合，需要是数值或数值数组类型	无
保留原始数据	是	是否保留原始列	开启

计算逻辑

• 通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，也是数学上用来降维的一种方法。
• 选择多列，进行PCA主成分分析，选择的列应是数值或数值数组类型。
• 指定输出结果的维度。

• PCA主成分分析预处理方式有：

  1. 无
  2. 中心化：将每个特征的均值调整成0。
  3. 标准化：在中心化的基础上将每个特征的标准差化成1。

使用示例

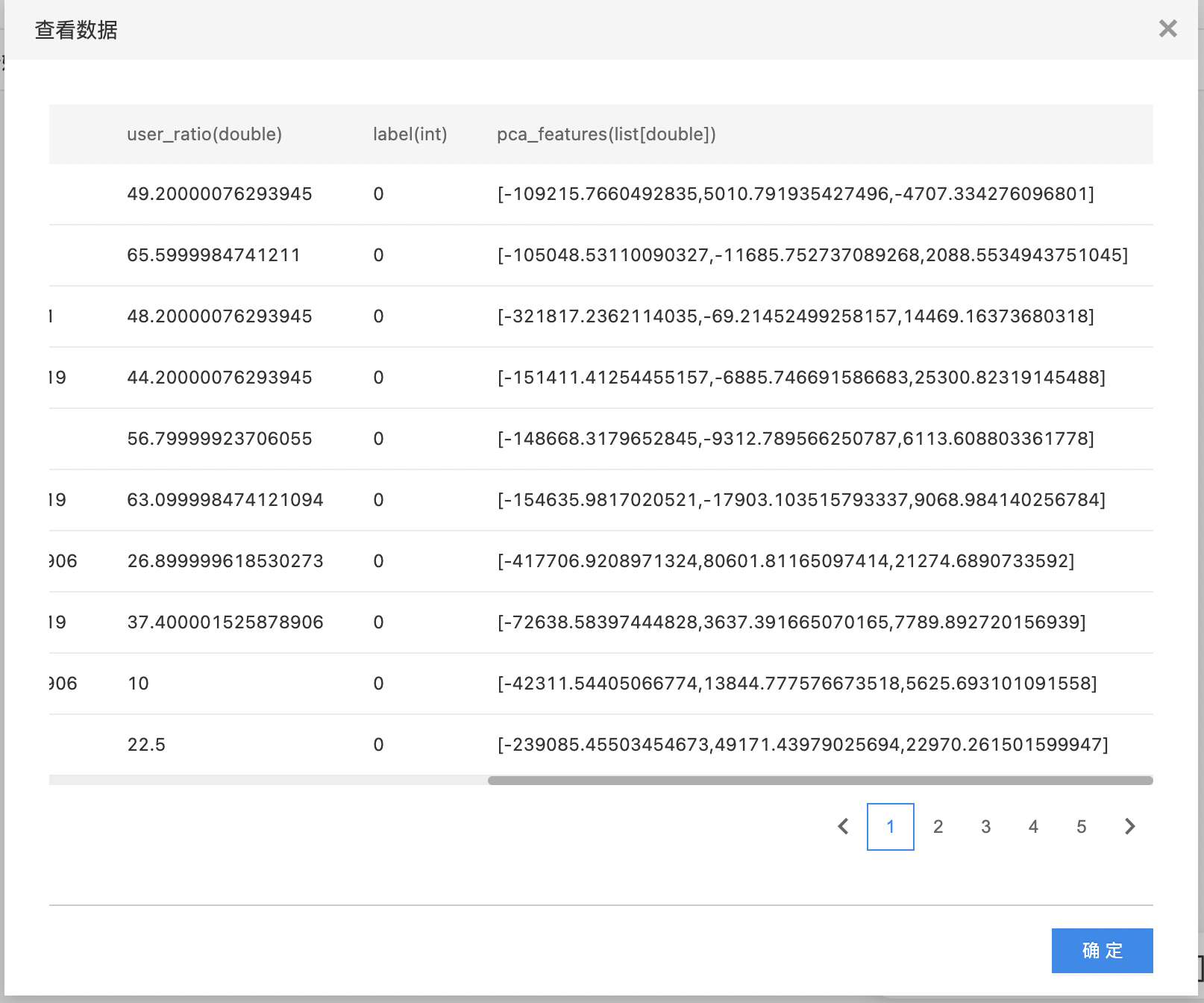
1. 如下图所示，构建算子结构，选择需要进行PCA主成分分析的列，填写结果维度。

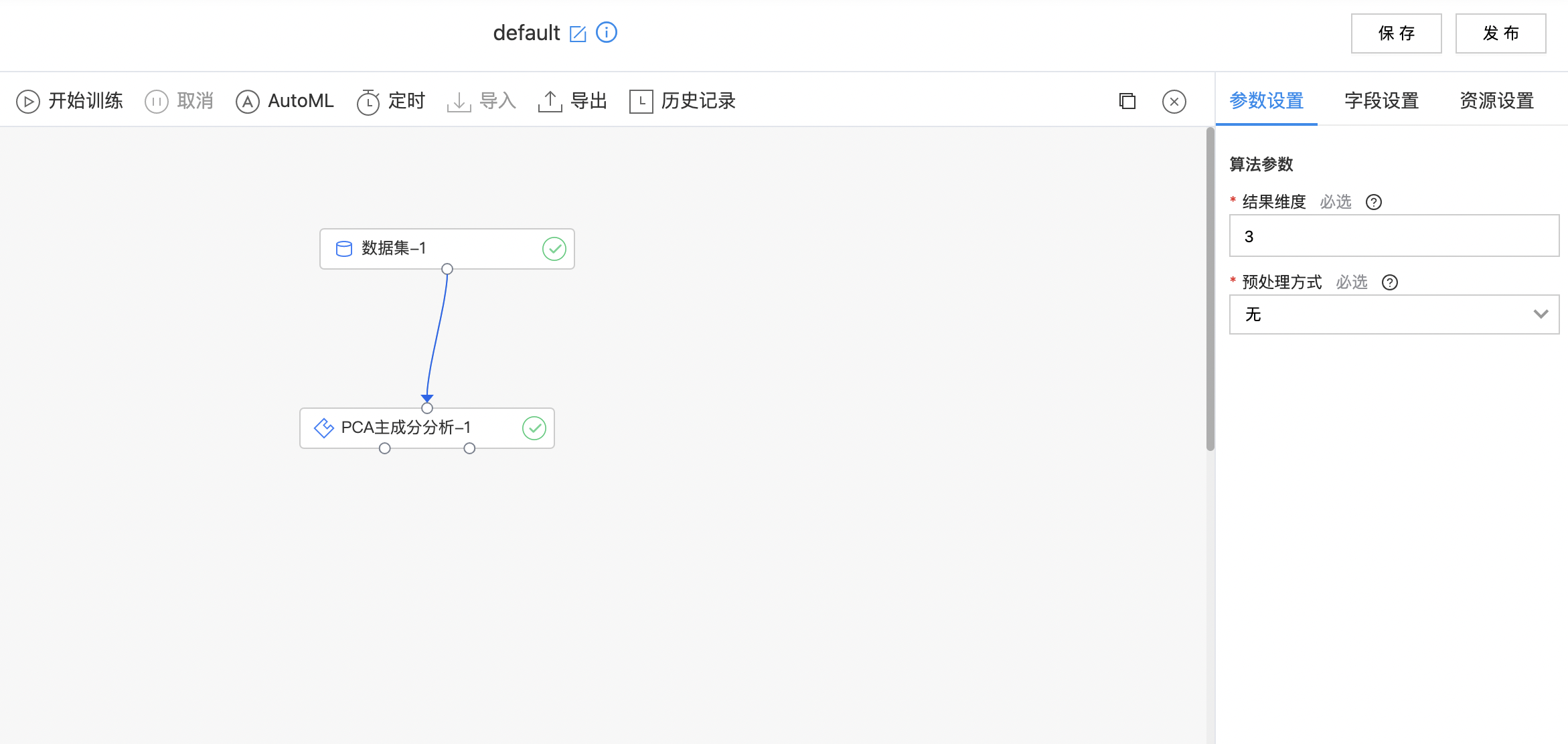
2. 查看PCA主成分分析的结果。

数值替换

对数据表中的一列，根据自定义的规则进行数值的替换，将符合规则的数值替换成新的数值。

输入

• 输入一个数据集和一条格式的替换指令。

输出

• 第一个输出是数值替换后的数据集。
• 第二个输出是数值替换模型。

算子参数

参数名称	是否必选	参数描述	默认值
替换指令	是	替换指令的每一条格式：列名[><=]值:替换值。如amount<10:9代表了把amount列中所有小于10的值转换成9。转换列支持数值和字符串类型；关系符号支持<, >, =, <=, >= 五种；列名、值、替换值只允许字母、数字和.-_三个特殊符号；替换值除了正常的值，还包括BML_MIN, BML_MAX, BML_MEAN三个特殊值，代表该列替换前的最小值、最大值和平均值。	无

使用示例

1. 拖入数据集组件选择数据集

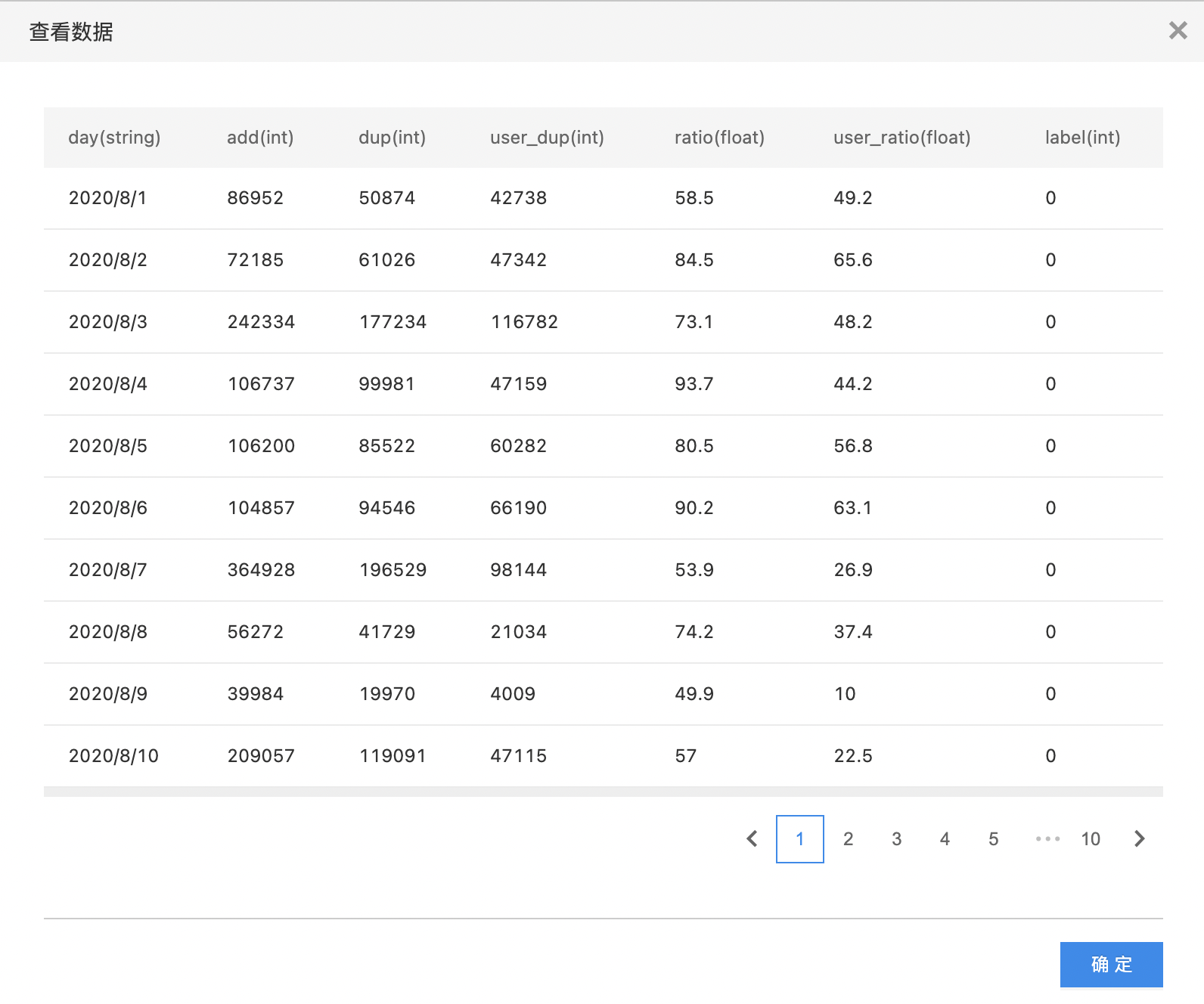
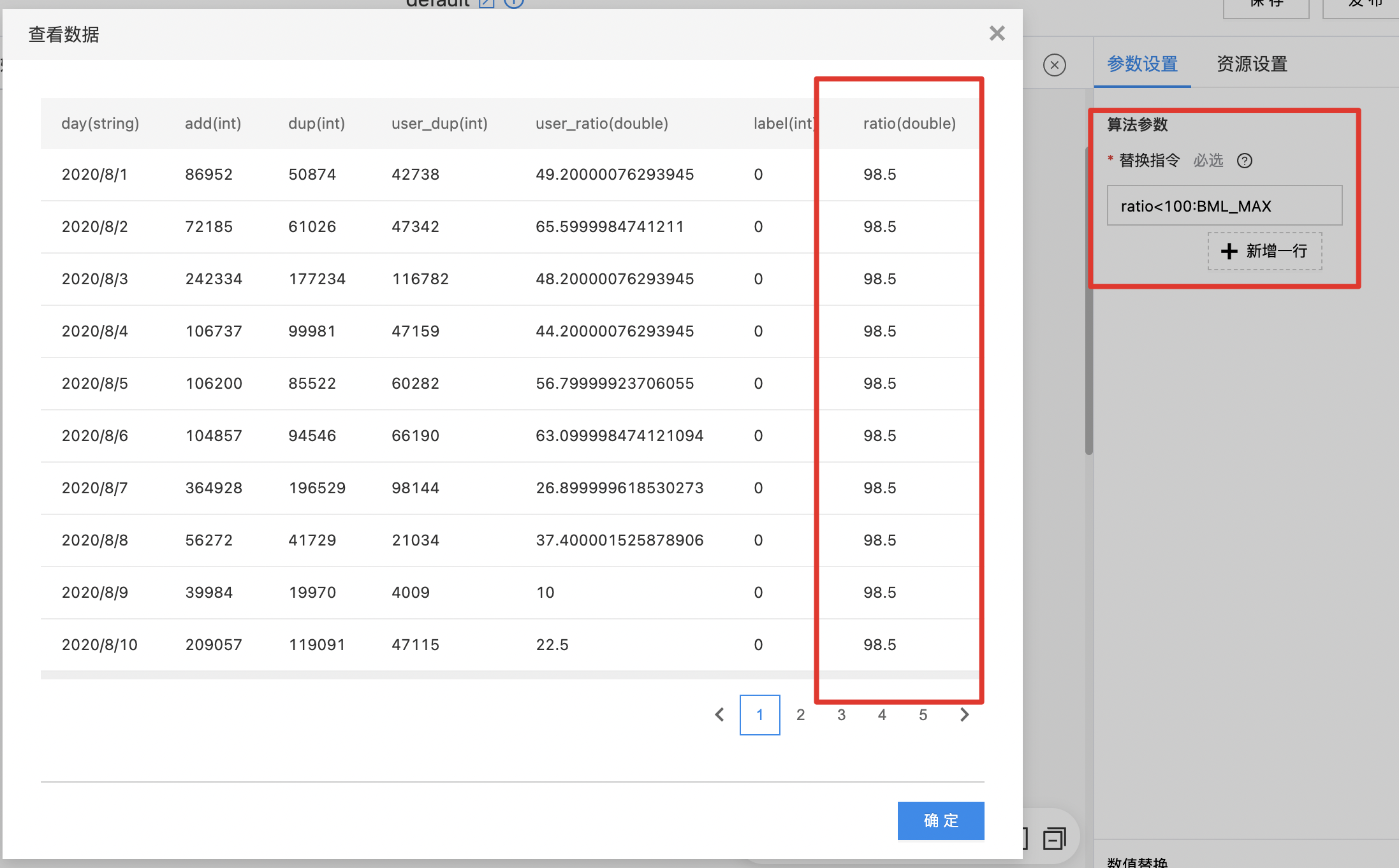
2. 拖入数值替换组件，连接数据集组件后，输入替换指令【ratio<100:BML_MAX】，即令ratio小于100的数值替换为该列最大的数值

归一化

对数据表中的一列或者多列，进行归一化处理，所选的列应是数值型或数值数组类型。

输入

• 输入一个数据集，选定需要归一化的列，选定归一化方法，选择是否保留原列。

输出

• 第一个输出是归一化后的数据集。
• 第二个输出是归一化的模型。

算子参数

参数名称	是否必选	参数描述	默认值
归一化方法	是	归一化方法,当前支持: 1.maxmin:0-1标准化 2.zscore:标准差标准化 3.logistic:使用logistic处理所选数据，范围(0,1) 4.lognormal:使用对数正态分布概率密度函数处理所选数据，范围(0,1) 5.tanH:使用tanH处理所选数据，范围(-1,1) 6.softmax:使用softmax处理所选数据，范围(0,1)	MAXMIN
是否保留原始列	是	是否保存原始列,状态为开启时，处理过的列重命名 "normalized_"前缀	关闭

字段参数

参数名称	是否必选	参数描述	默认值
归一化列	是	需要归一化的列集合，需要是数值或数值数组类型

计算逻辑

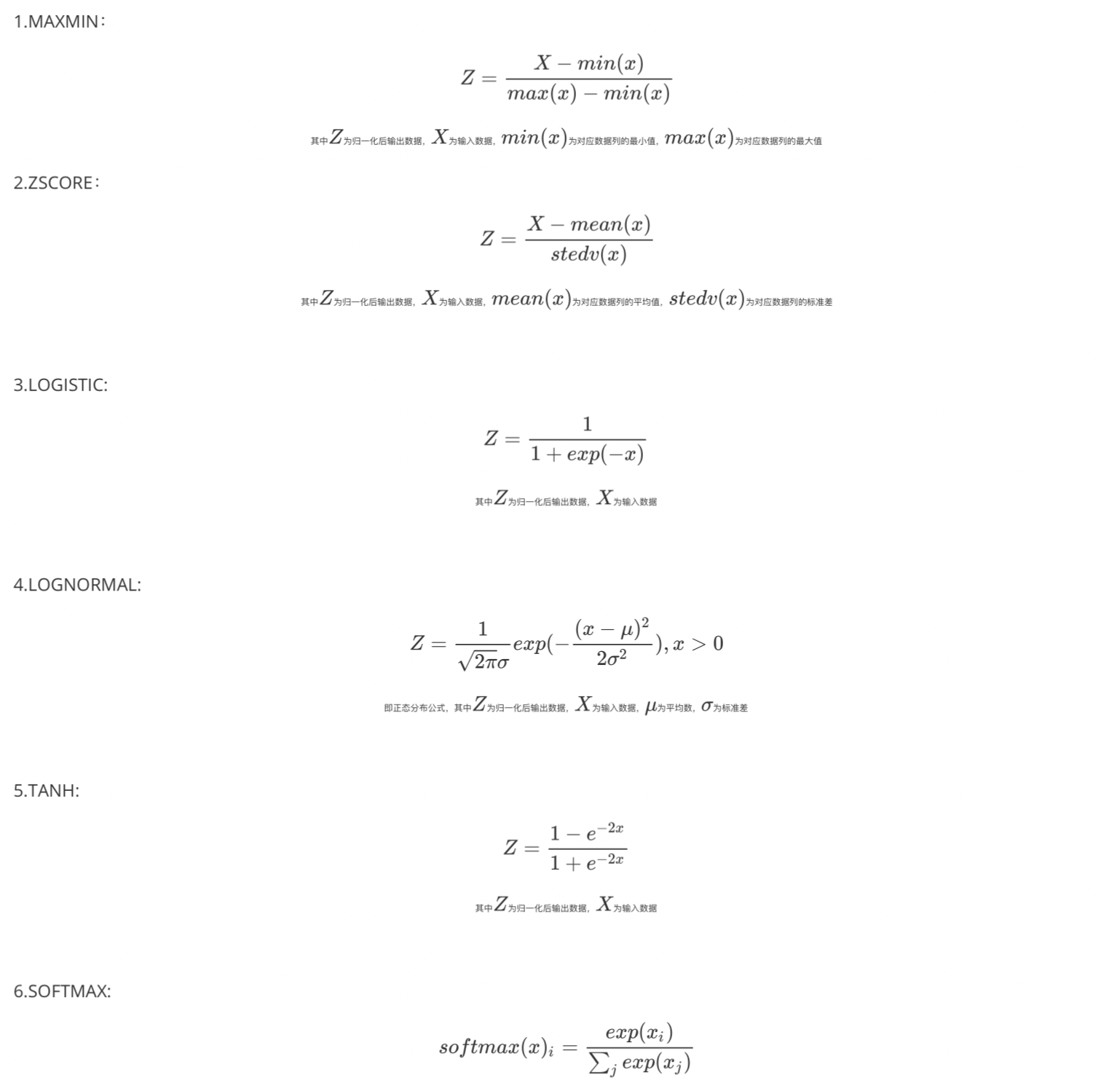
示例

假设当前有一列特特征值分别为[1，5，3]，对应的softmax归一化输出值如下:

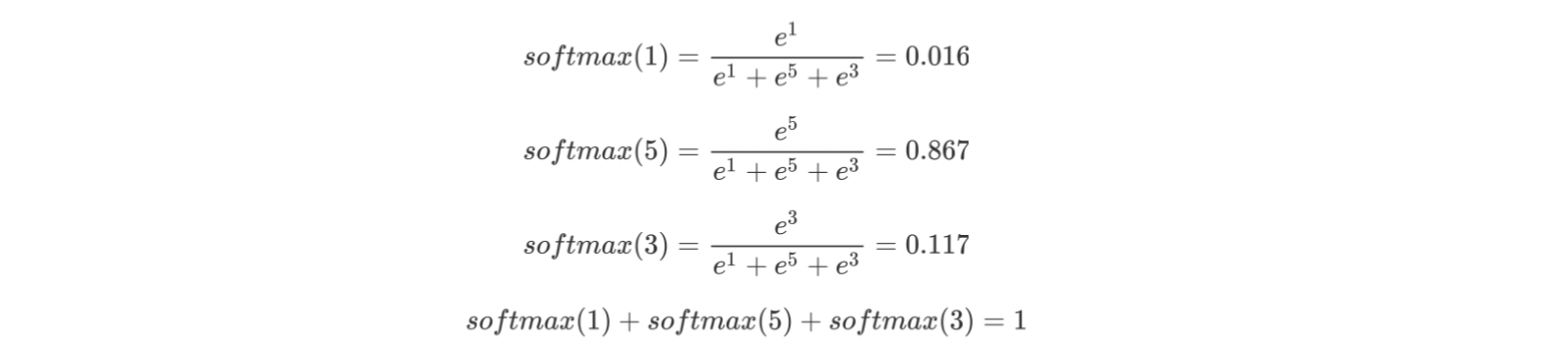
使用示例

1. 如下图所示，构建算子结构，选择需要归一化的列，选择归一化方法。

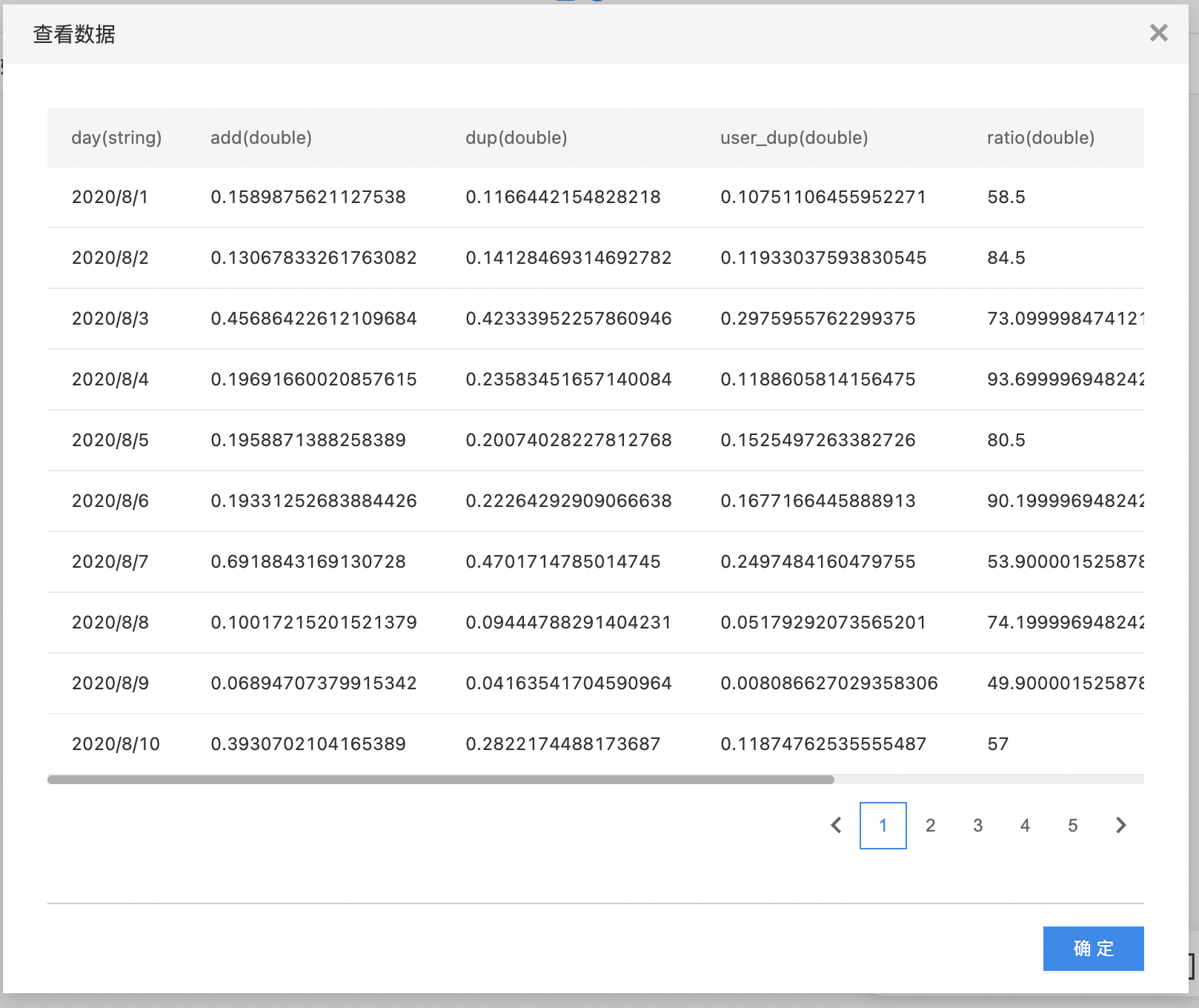
2. 查看归一化的结果。

直方映射

直方图编码，主要针对类别型特征与类别型标签的一种特征编码方式。

输入

• 输入一个数据集，选择需要直方编码的列集合与标签列。

输出

• 第一个输出是结果数据集。
• 第二个输出是直方映射变换（Transformation），后续可以使用这个变换操作其它数据集。

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	需要直方编码的列集合，要求是整型、长整型、字符串，唯一值不超过500。	无
标签列	是	标签列只能数值类型	无
保留原始列	是	是否保留原始列

计算逻辑

使用示例

1. 如下图所示，构建算子结构，选择需要直方映射的列。

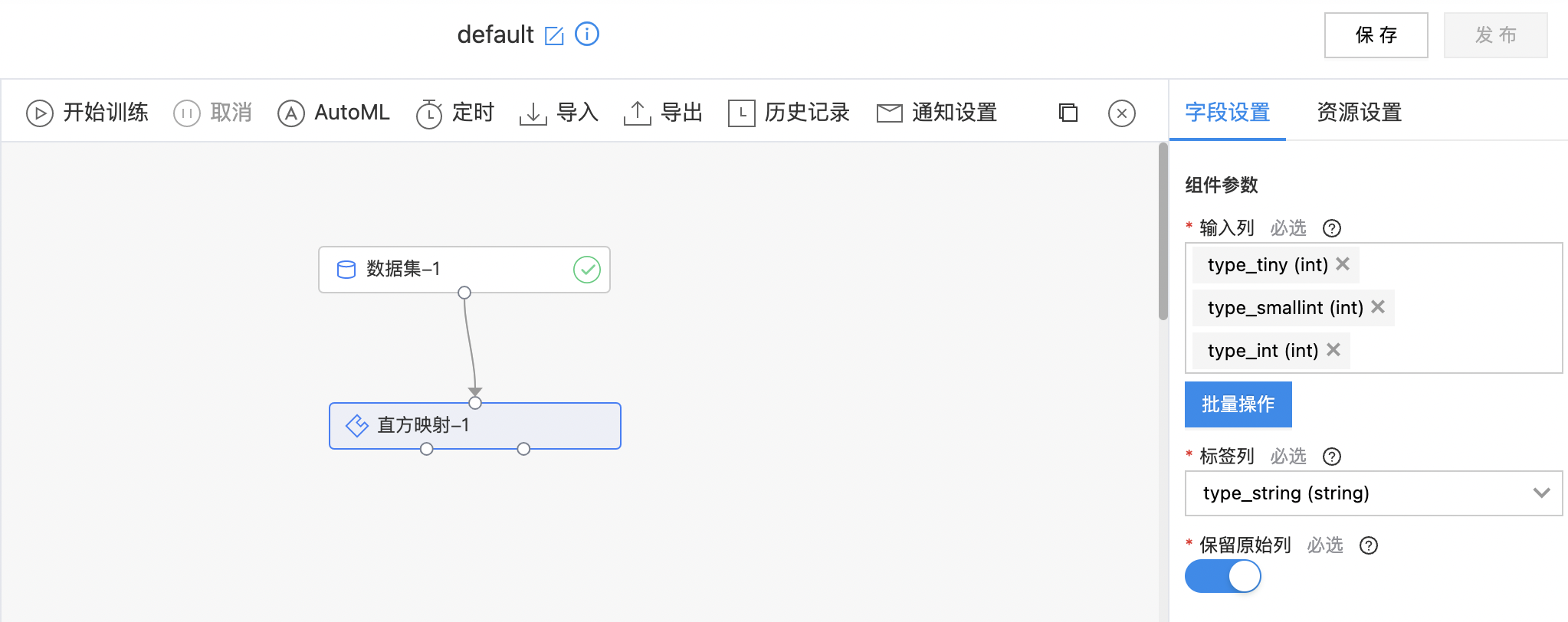
2. 查看直方映射的结果。

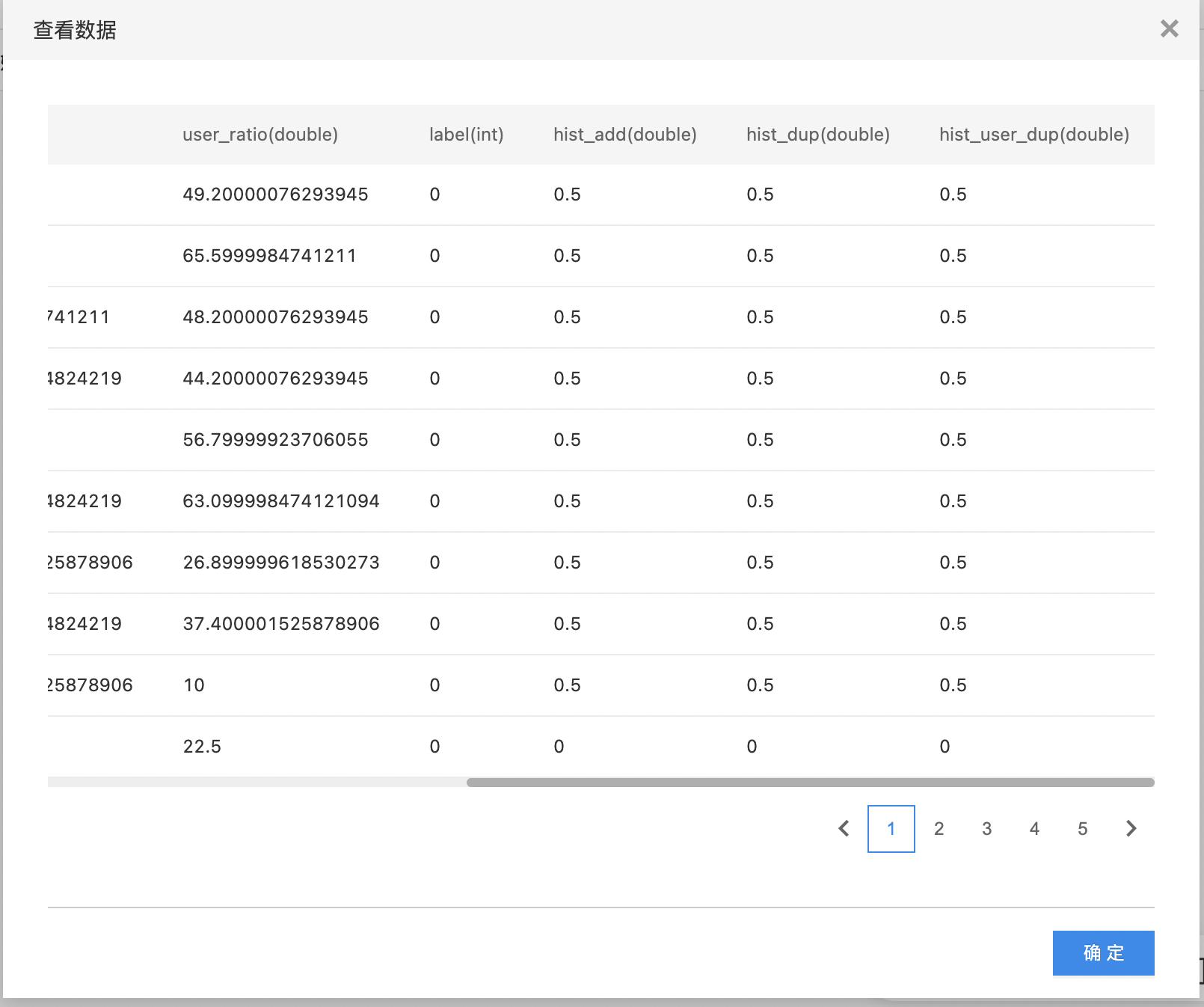
woe编码

WOE是一种有监督的编码方式,将预测类别的集中度的属性作为编码的数值，编码仅仅针对于二分类问题。

输入

• 输入一个数据集，需要选择要做woe编码的列，可以选择一列或多列。

输出

• 第一个输出是结果数据集，在输入数据集的基础上添加了"woe_选择的列名"列，列的类型是double。
• 第二个输出是woe编码变换（Transformation），后续可以使用这个变换操作其它数据集；若测试集的对应特征列存在值未在训练集中出现，则对应的值woe编码为null。

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	需要woe编码的列集合，要求是整型、长整型、字符串。	无
标签列	是	标签列只能是0-1变量；1表示响应；要求是数值类型、字符串。	无

计算逻辑

woe计算公式：

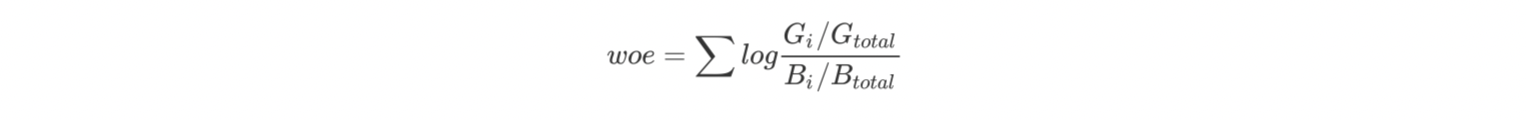
其中G和B为样本的类别。

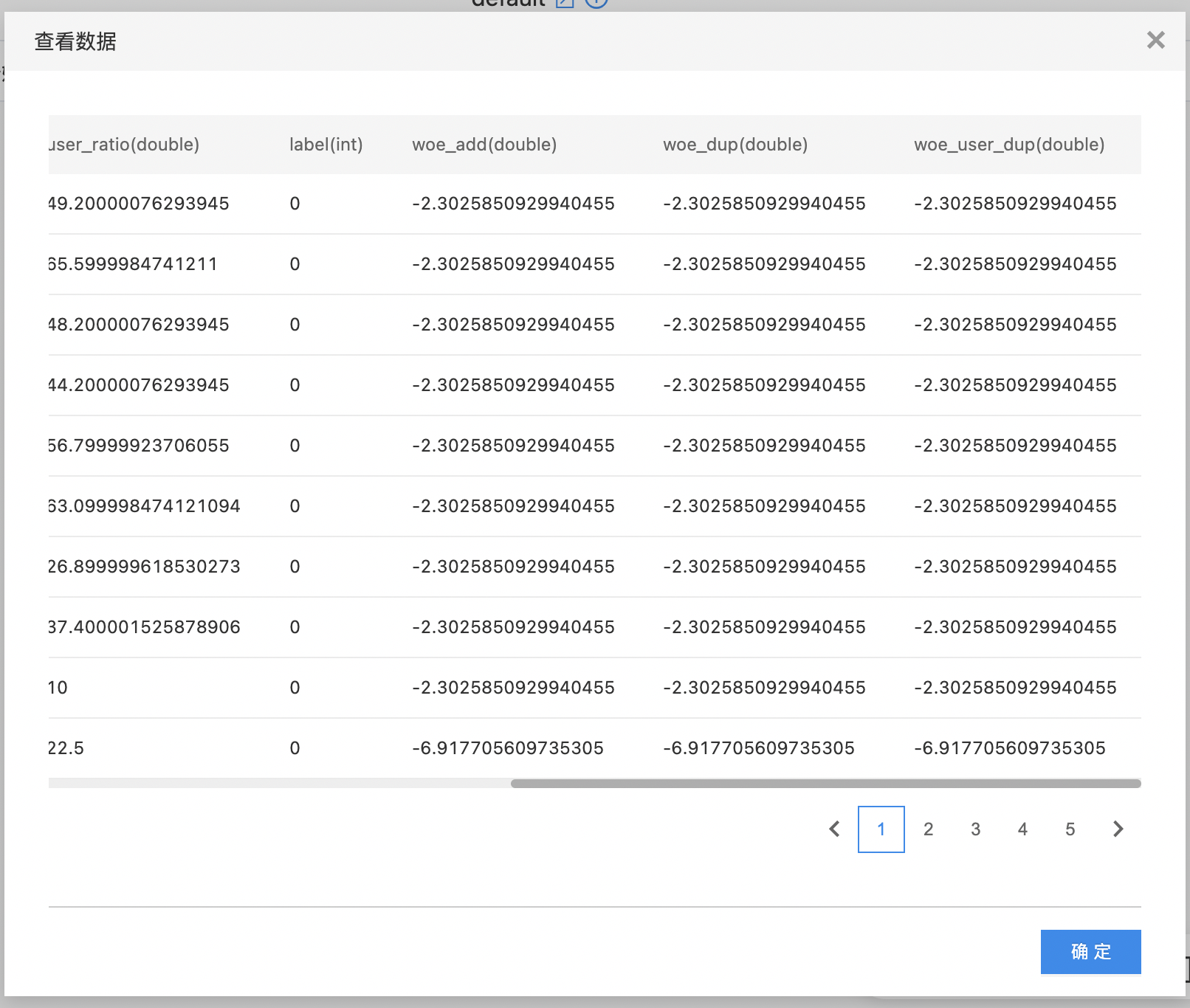
使用示例

1. 如下图所示，构建算子结构，选择需要进行woe编码的列。

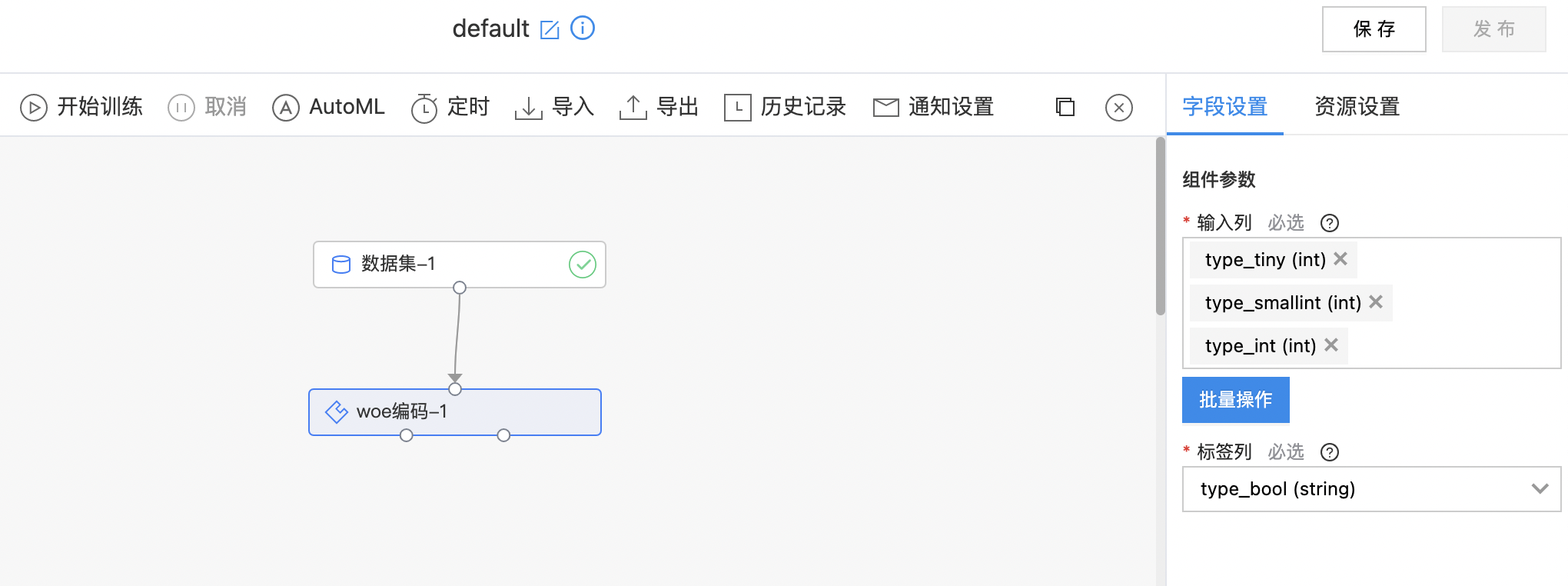
2. 查看woe编码结果。

嵌入式特征选择

嵌入式特征选择是在学习器训练过程中自动进行特征选择，特征选择算法本身作为组成部分嵌入到学习算法里。

输入

• 输入一个数据集，选择要做嵌入式特征选择的列，选择特征选择的方法与条件。

输出

• 第一个输出是结果数据集，在输入数据集的基础上去除不重要的特征列。
• 第二个输出是嵌入式特征选择变换（Transformation），后续可以使用这个变换操作其它数据集。

算子参数

参数名称	是否必选	参数描述	默认值
监督模式	是	根据监督任务类型，给出估计器类型（分类/回归）	分类
分类估计器	是	选择分类算法： GBDT分类 逻辑回归(内置交叉验证)+L1正则 随机森林分类 SVM分类	逻辑回归(内置交叉验证)+L1正则
回归估计器	是	选择回归算法： GBDT回归 LASSO(内置交叉验证) 随机森林回归 SVM回归	LASSO(内置交叉验证)
交叉验证折数	是	交叉验证折数，必须不小于2。对于分类任务，交叉验证折数不能大于每个类别的样本个数；若不能确定交叉验证折数是否大于每个类别的样本个数，建议将交叉验证折数设置小一点， 范围：[2, 20]。	5
特征阈值选择模式	是	用于特征选择的阈值输入模式。特征重要性不小于阈值，保留对应特征，否则丢弃。有三种模式：自动选择、自定义字符串、自定义浮点数。对于自动选择模式，如果估计器的参数惩罚被显示或隐式地设置为L1(例如Lasso)，则使用的阈值为1e-5；否则，默认使用“mean”	自动选择
自定义浮点数	是	阈值浮点数格式输入	0.25
自定义字符串	是	阈值字符串格式输入。既可以字符串”mean”、”median”，分别边表示所有特征重要性的平均数、中位数，也可以是浮点数和mean或median相乘对应的字符串，例如”1.25*mean”,表示mean或median乘以一个缩放因子	mean

字段参数

参数名称	是否必选	参数描述	默认值
特征列	是	嵌入式特征选择使用的特征列，要求必须是数值类型。	无
标签列	是	嵌入式特征选择目标列，分类任务：要求是整数或字符串类型，回归任务：需要是数值类型。	无

计算逻辑

嵌入式特征选择分为基于惩罚项与基于树模型两大类，线性模型的损失函数增加惩罚项进行稀疏处理，即重要性小的特征系数迭代为0，进而达到特征选择的目的，进而达到特征选择的目的；树模型根据子节点纯度判断特征选择的优劣，达到特征选择的目的，用户可以根据自身需求自行选择具体的线性模型或树模型。

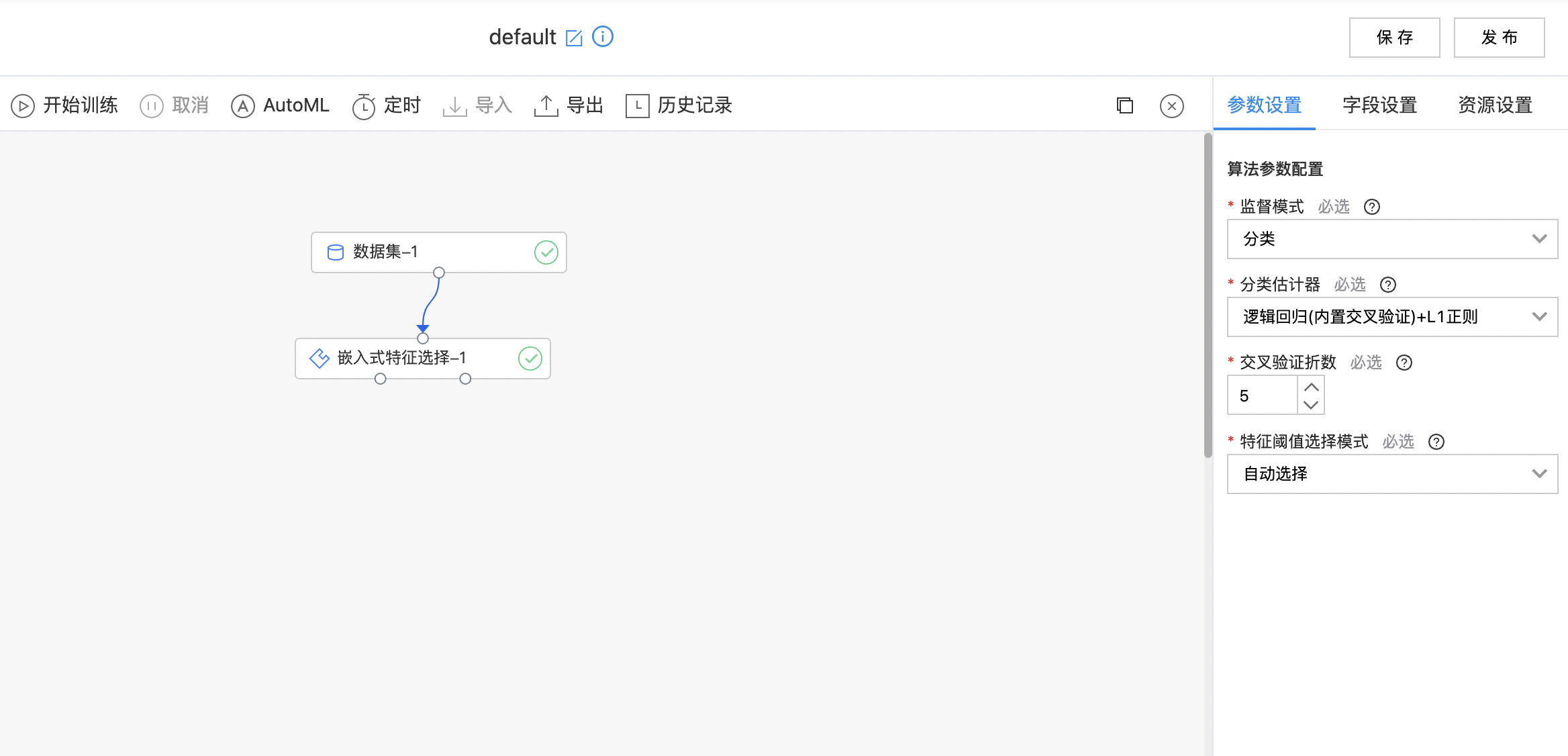
使用示例

如下图所示，构建算子结构，选择需要进行特征选择的列，配置选择方法。

FastICA

独立成分分析（Independent Component Analysis，ICA）是一种从多维数据中寻找其具有内在独立性和非高斯性因子的数据处理方法。ICA可以在未知源信号及混合矩阵信息的情况下分离出相互统计独立的源信号，FastICA是基于负熵的快速独立分量分析算法。

独立分量分析将多变量信号分解为独立性最强的加性子组件。 它通过Fast ICA算法在 scikit-learn 中实现。 ICA 通常不用于降低维度，而是用于分离叠加信号。 由于 ICA 模型不包括噪声项，因此要使模型正确，必须使用白化(whitening)。这可以在内部使用 whiten 参数或手动使用 PCA 的一种变体，ICA 通常用于分离混合信号（称为盲源分离的问题）。

输入

• 输入一个数据集，需要选择数据集的特征列。

输出

• 第一个输出是结果数据集。
• 第二个输出是FastICA模型，需要连接Python特征工程预测组件，进行预测，如果选择不保留原始列，输出数据集中删去原始列。

算子参数

参数名称	是否必选	参数描述	默认值
降维后的维度	是	降维后的维度，该值应大于0且小于等于选择的特征个数；当出现infs or NaNs错误时请将请尝试调小该值，或者调整随机种子和开启白化。	2
迭代次数	是	最大迭代次数 范围：[1, inf)。	200
白化	是	白化是一种重要的预处理过程，其目的是为了降低输入数据的冗余性，使得经过白化处理的输入数据特征之间相关性较低, 所有特征具有相同的方差。	开启
随机数种子	是	随机数种子是为了保证每次随机的结果都是一样的 范围：[0, inf)。	0

字段参数

参数名称	是否必选	参数描述	默认值
特征列	是	ICA使用的特征列，最少选择两列，要求必须是数值类型	无
保留原始列	是	是否保留原始列	开启

使用示例

1. 如下图所示，构建算子结构，选择特征列，配置算法参数。

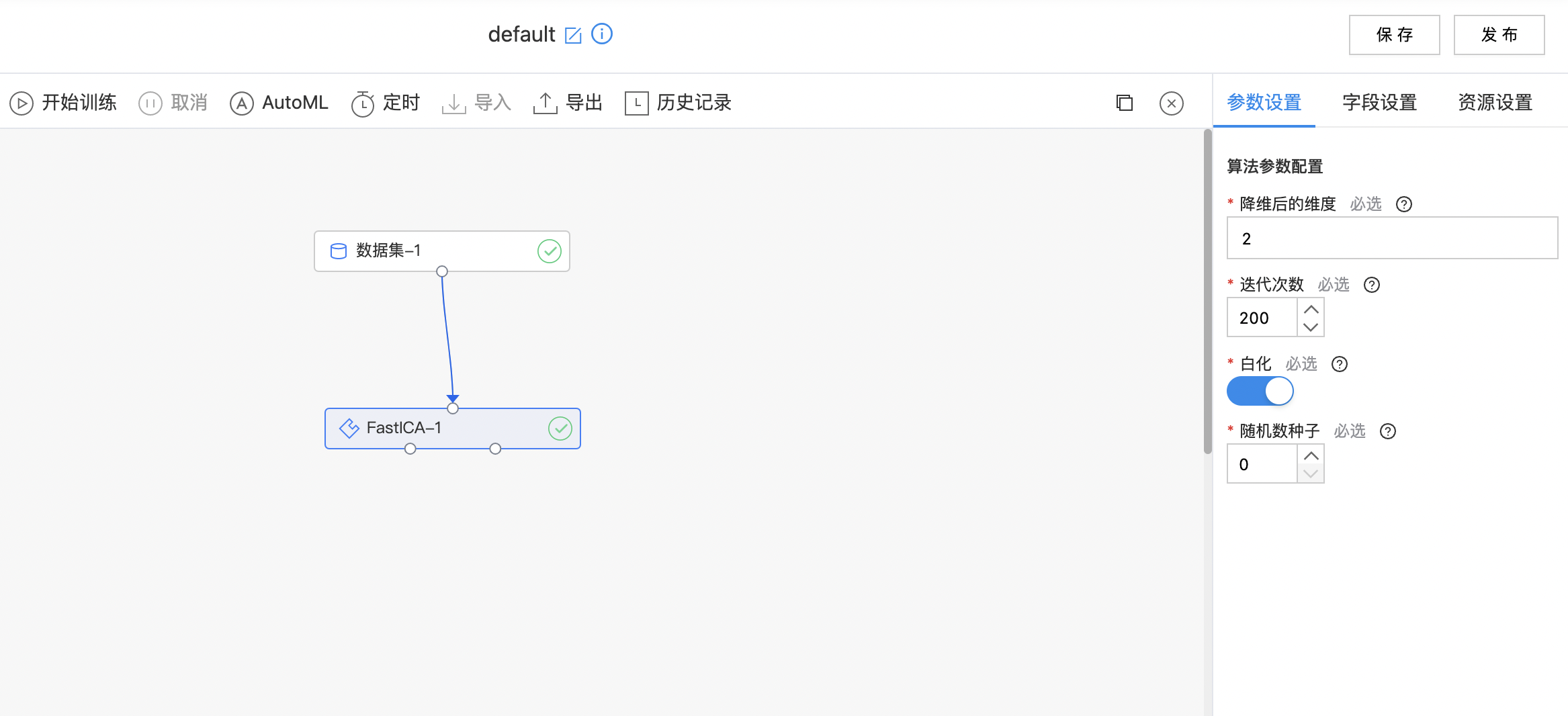
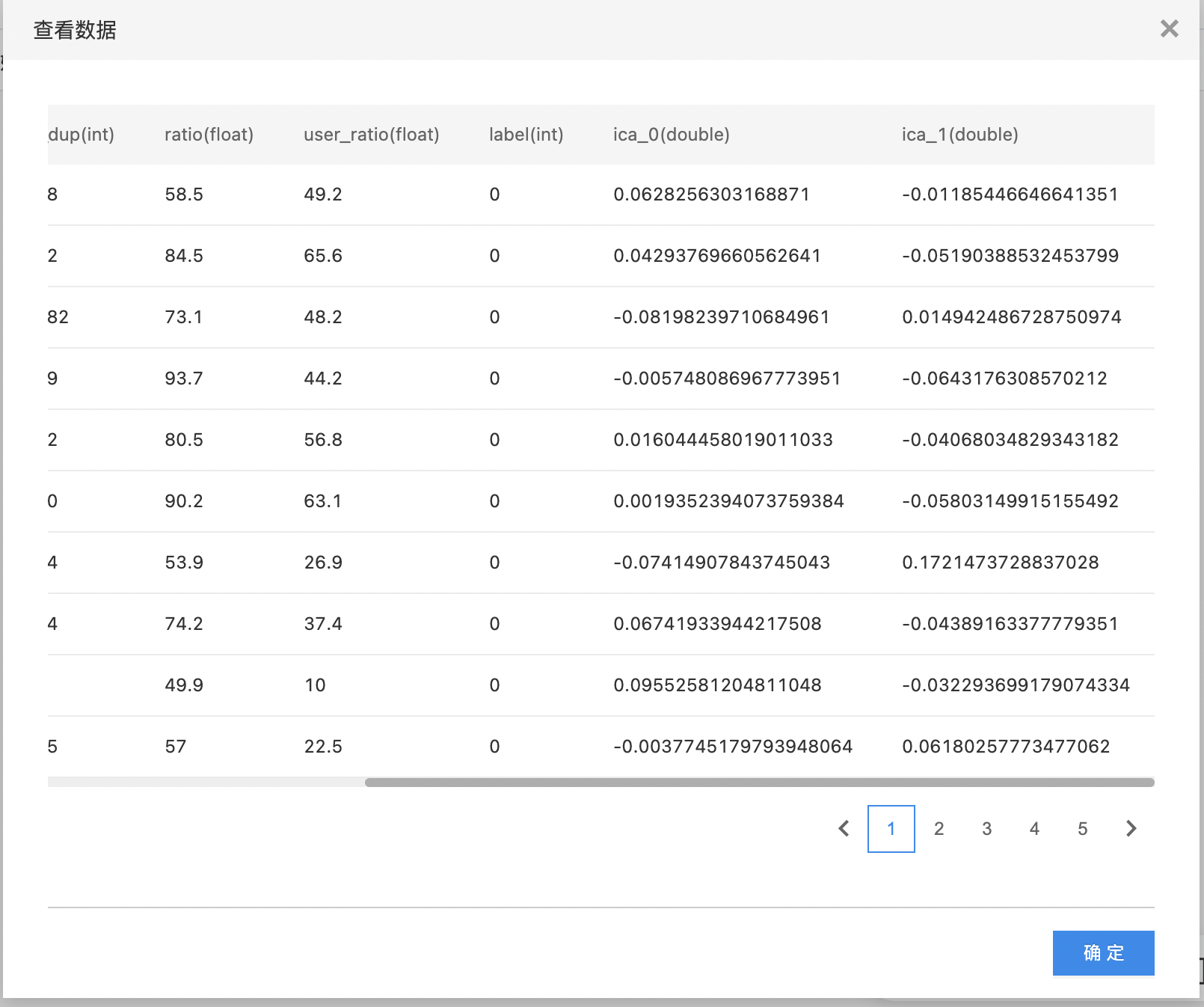
2. 查看FastICA结果。

LDA

线性判别分析（LDA）是一种经典的线性学习方法，在二分类问题上因为最早由 Fisher 提出，亦称“Fisher 判别分析”。 LDA 的思想非常朴素：给定训练样本集，设法将样本投影到一条直线上，使得同类样本的投影点尽可能接近、异类样本的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。

输入

• 输入一个数据集，数据集的特征列double/int，标记列是Double或Int类型。

输出

• 第一个输出是结果数据集。
• 第二个输出是Python预测模型，需要连接Python特征工程预测组件进行预测。

算子参数

参数名称	是否必选	参数描述	默认值
最优化算法	是	求解最优化问题的算法： svd eigen	svd
降维后的维度	是	降维后的维度，该值应小于标签列类别数-1，降维后的维度为该值和标签列类别数-1之间的最小值	2

字段参数

参数名称	是否必选	参数描述	默认值
特征列	是	LDA使用的特征列，最少选择两列，要求必须是数值类型	无
标签列	是	LDA目标列，要求是整数或字符串类型	无

使用示例

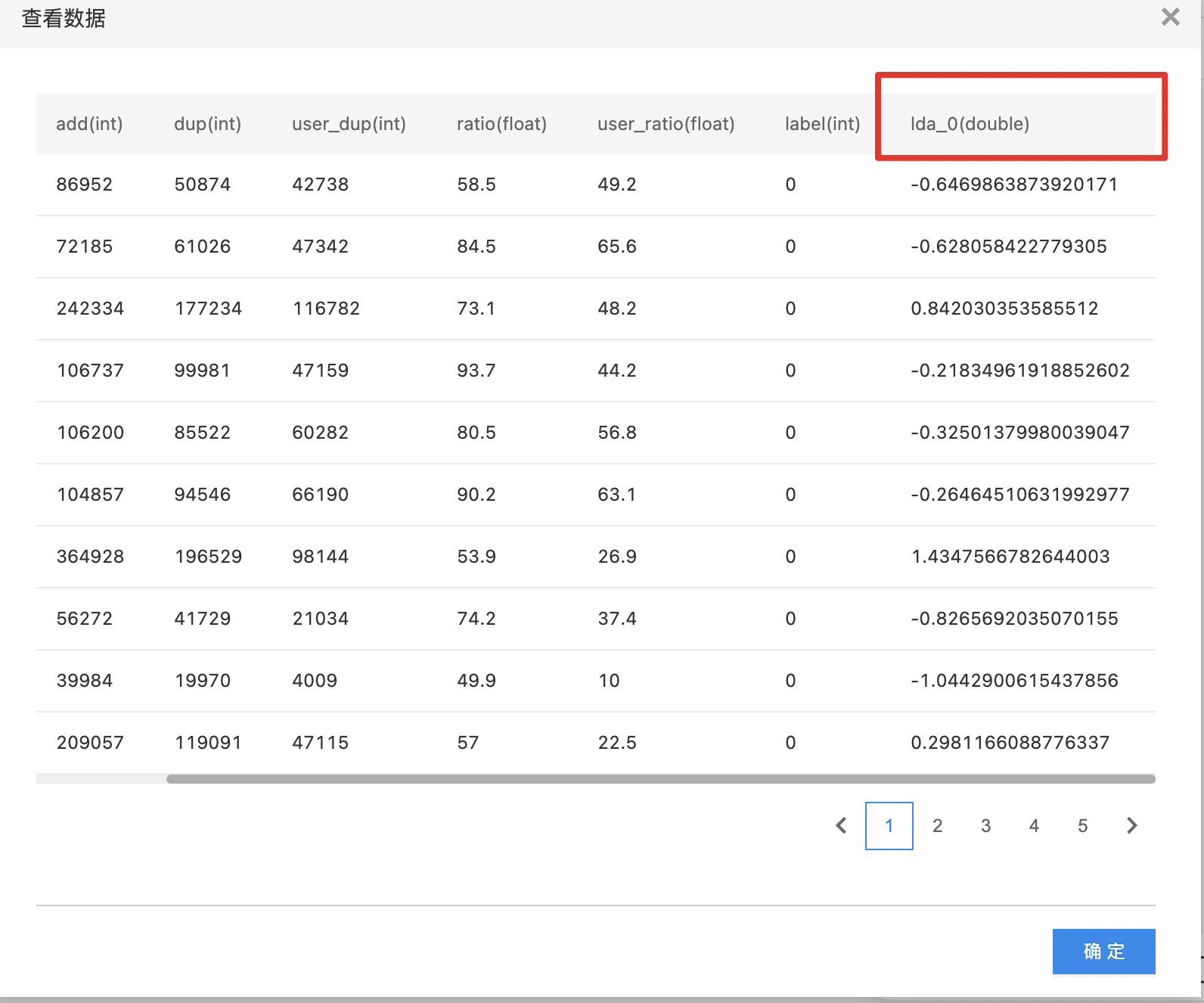
1.如下图所示，构建算子结构，选择需要进行LDA处理的列。

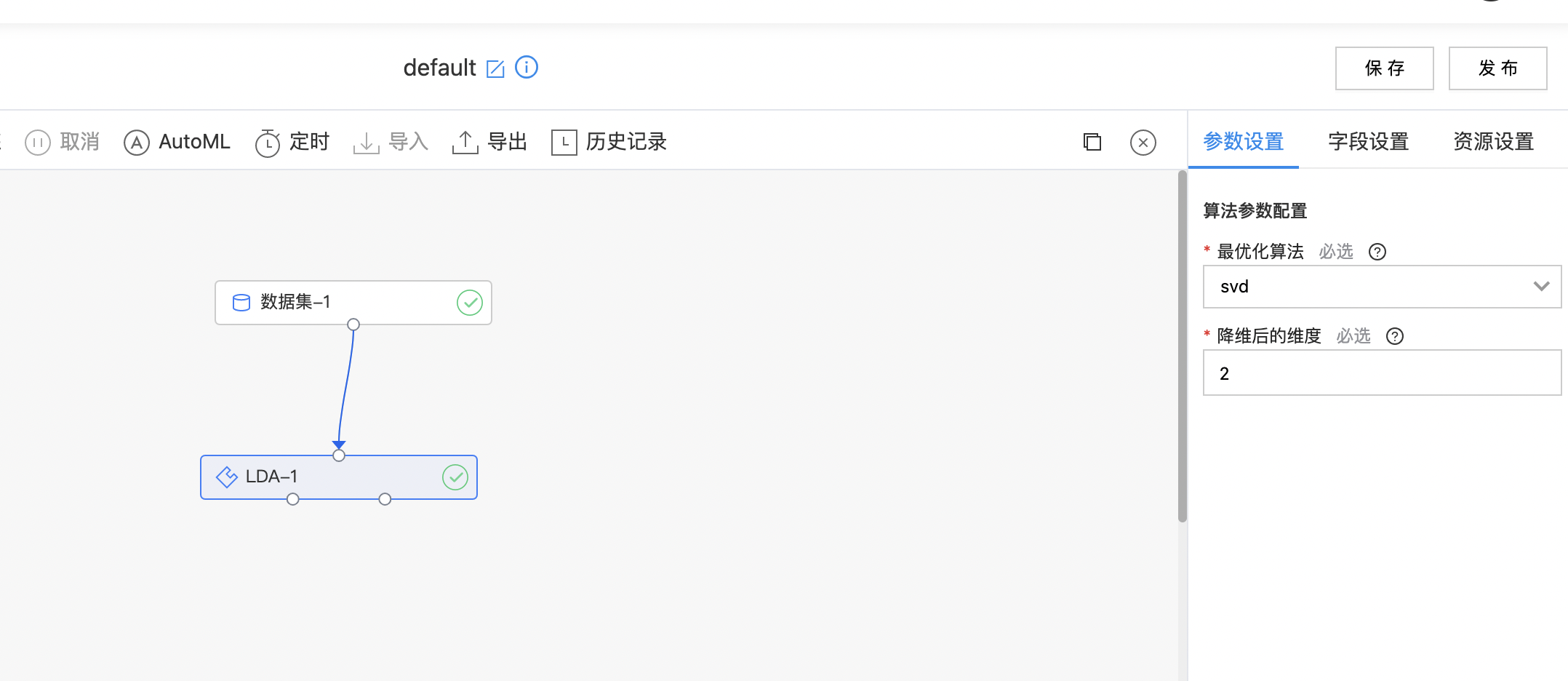
2.查看LDA的结果。

OrdinalEncoder(单机)

OrdinalEncoder的功能是将类别特征(categorical features)变为有序数值特征(ordinal integers)。

输入

• 输入一个数据集，指定输入列。

输出

• 第一个输出是结果数据集，模型在原数据集的基础上添加了k列（设k是输入列的个数），类型为整数，名称是对应输入列加上前缀"ordinalencoder_", 如果选择不保留原始列，输出数据集中或删去原始列。
• 第二个输出是OrdinalEncoder(单机)模型。

字段参数

参数名称	是否必选	参数描述	默认值
输入列	是	OrdinalEncoder使用的特征列，要求数值、字符类型	无
保留原始列	是	是否保留原始列	开启

计算逻辑

假设输入X = [['Male', 1], ['Female', 3], ['Female', 2]]，这里输入数据中含有两列，说明有两类特征，第一列取值范围为：[ 'Female'，'Male']，按照顺序编码为[0,1]，第二列取值范围为：[1,2,3],编码结果为[0,1,2]。按照这个思路，['Female', 3], ['Male', 1]的顺序编码分别为[0,2]和[1,0]

使用示例

1. 如下图所示，构建算子结构，选择特征列。

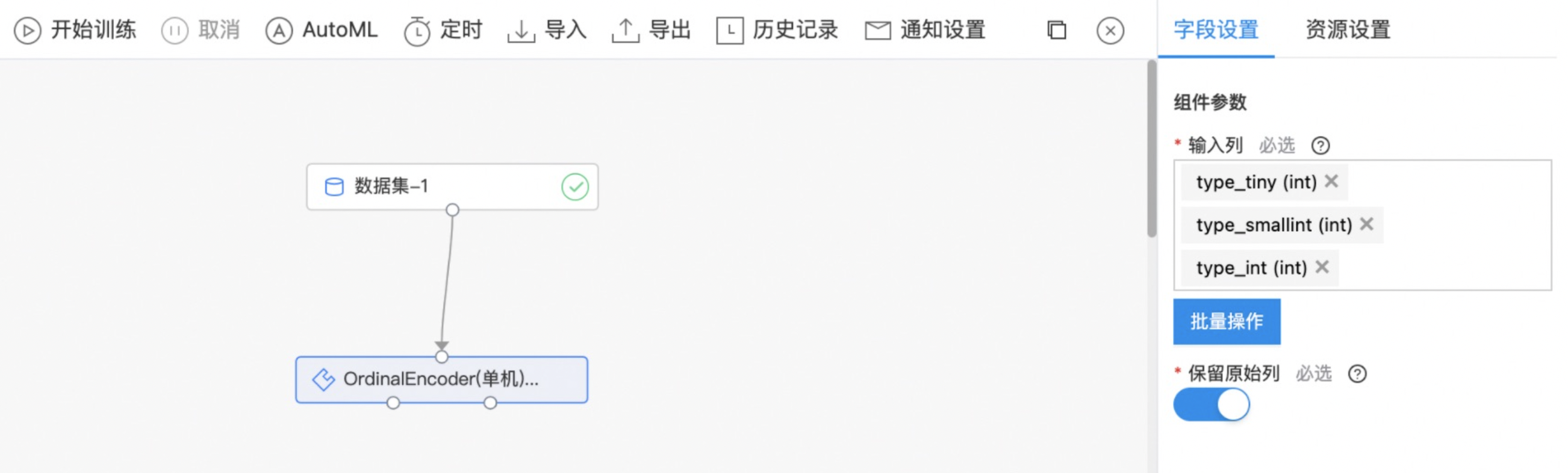
2. 查看OrdinalEncoder(单机)的结果。

尺度变换

数值型特征的数据转换，目前包括 对数，指数，box-cox。

输入

• 输入一个数据集，用户需要选择要做尺度变换的列，选择的列的类型需要是数值类型。

输出

• 第一个输出是结果数据集，在输入数据集的基础上添加名为"变换模式前缀_选择列"的特征列，变换模式前缀：对数（log_base）/指数（exp_base）/box-cox（box_cox）。
• 第二个输出是尺度变换变换（Transformation），后续可以使用这个变换操作其它数据集。

算子参数

参数名称	是否必选	参数描述	默认值
尺度变换模式	是	支持变换：对数/指数/box-cox	对数
指数基底	否	支持以2/e为底	e
对数基底	否	支持以2/e/10为底	e
参数lmbda选择模式	否	支持两种选择模式：自动选择（默认）、自定义标量。自动选择：找到最大化对数似然函数的lambda，自定义标量：自定义参数lmbda值	自动选择
自定义标量	否	整数或浮点数格式输入	0

字段参数

参数名称	是否必选	参数描述	默认值
尺度变换列	是	尺度变换的列集合，要求是数值类型	无

计算逻辑

box-cox计算公式：

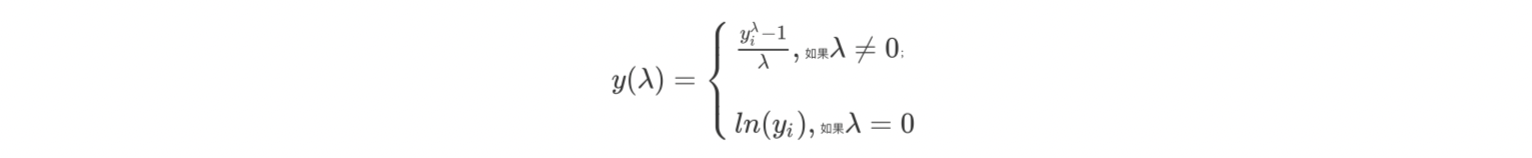
其中λ即为算子参数中的lmbda值。

使用示例

1. 如下图所示，构建算子结构，选择需要尺度变换的列，选择变换方式。

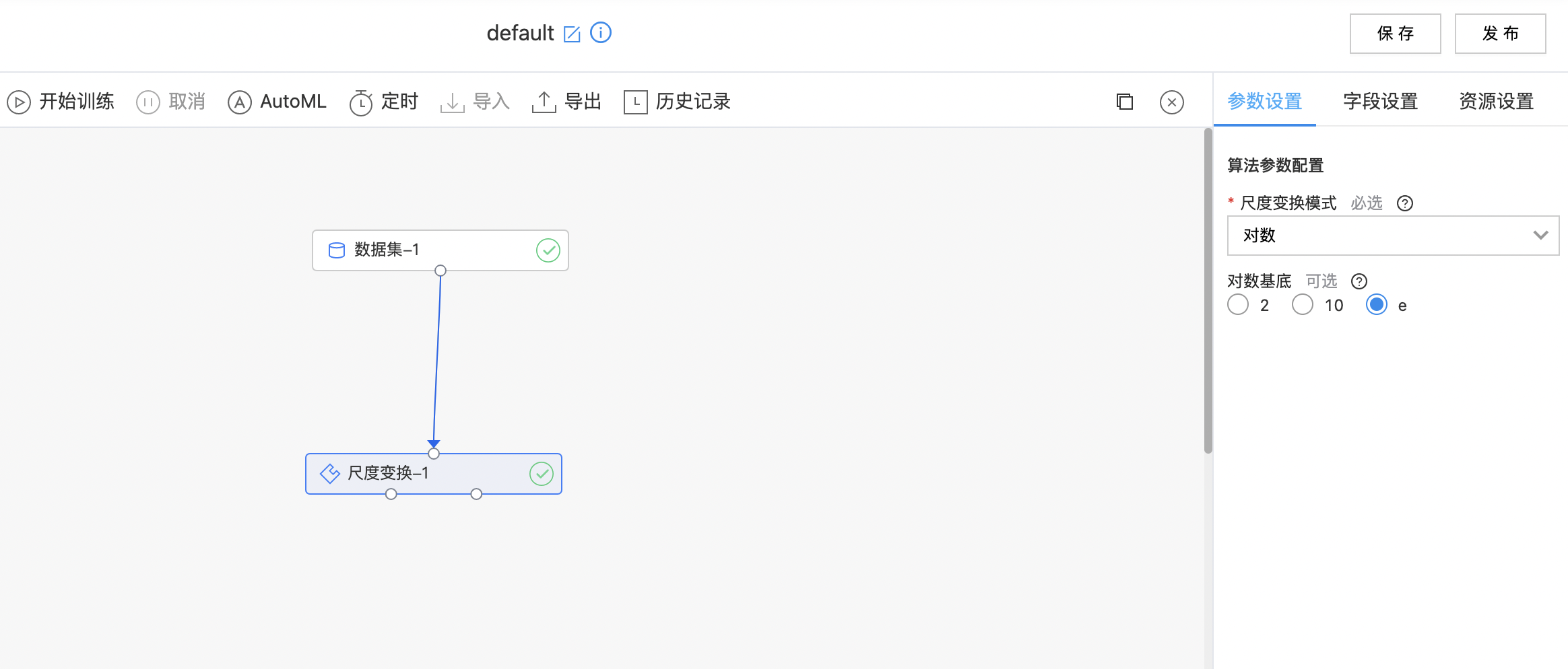
2. 查看尺度变换的结果。

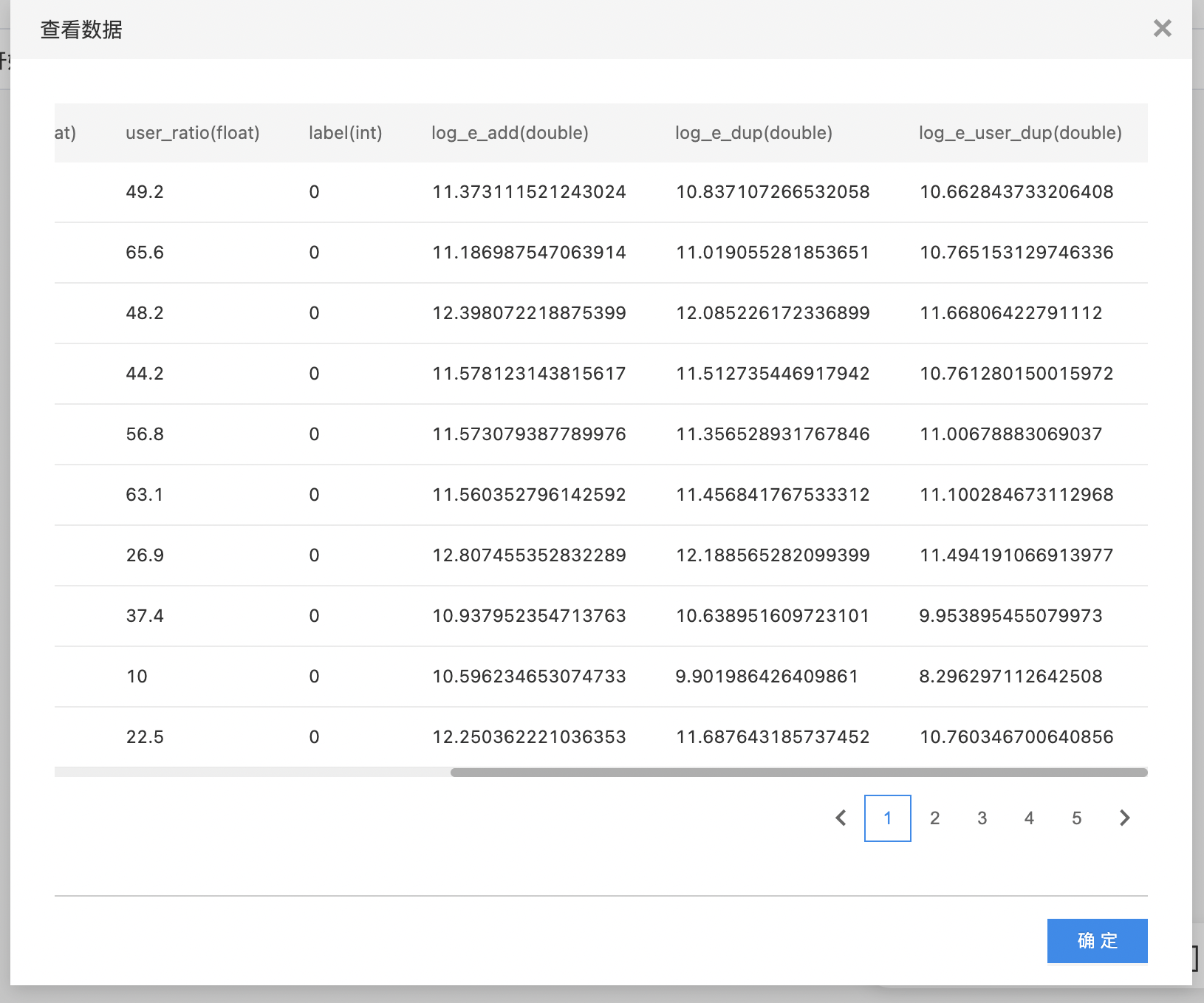
包装式特征选择

包装式特征选择基于贪婪搜索算法，因为它们会评估特征的所有可能组合，并为特定的机器学习算法选择能产生最佳结果的组合，例如用户需要训练一个随机森林的模型，算子参数选择随机森林，那么算子输出的特征集即为最优的特征选择结果。这种方法的缺点是测试所有可能的特征组合可能在计算上非常昂贵，尤其是在特征集非常大的情况下。

输入

• 输入一个数据集，选择要做包装式特征选择的列，选择特征选择的方法与条件。

输出 

• 第一个输出是结果数据集，在输入数据集的基础上消除不重要的特征列。
• 第二个输出是包装式特征选择变换（Transformation），后续可以使用这个变换操作其它数据集。

算子参数

参数名称	是否必选	参数描述	默认值
监督模式	是	根据监督任务类型，给出估计器类型（分类/回归）	分类
分类估计器	是	选择分裂算法： GBDT分类 逻辑回归 随机森林分类	逻辑回归
回归估计器	是	选择回归算法： GBDT回归 线性回归 随机森林回归	线性回归
特征排除步长	是	若值不小于1，表示每次迭代排除（值取整）特征个数；若值(0.0，1.0)之间，表示每次迭代按比例排除特征。 范围：[0.1, inf)	1
交叉验证折数	是	交叉验证折数，必须不小于2。对于分类任务，交叉验证折数不能大于每个类别的样本个数；若不能确定交叉验证折数是否大于每个类别的样本个数，建议将交叉验证折数设置小一点。 范围：[2, 20]	5

字段参数

参数名称	是否必选	参数描述	默认值
特征列	是	包装式特征选择使用的特征列，要求必须是数值类型	无
标签列	是	包装式特征选择目标列。分类任务：要求是整数或字符串类型，回归任务：需要是数值类型	无

使用示例

1. 如下图所示，构建算子结构，选择需要进行特征选择的列，配置选择方式。

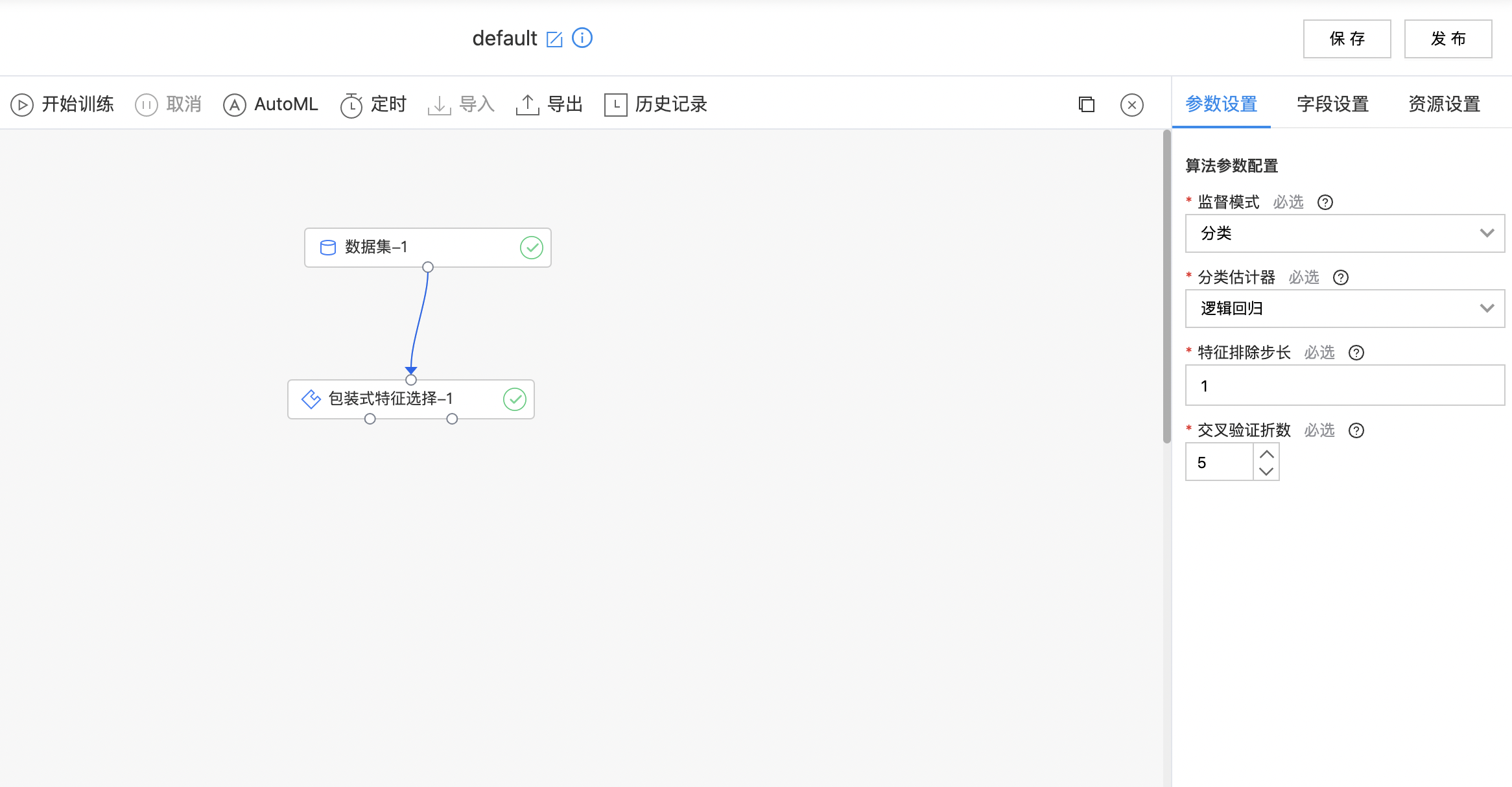
自定义Python特征工程(单机)

自定义编写Python代码进行特征工程处理。

输入

• 输入一个数据集，需要编写Python代码处理特征。

输出

• 第一个输出是结果数据集。
• 第二个输出是自定义 python 特征工程变换(单机)模型，后续可以使用这个变换操作其它数据集。

算子参数

参数名称	是否必选	参数描述	默认值
Python代码编辑窗口	是	在编辑窗口中编辑数据处理脚本	无

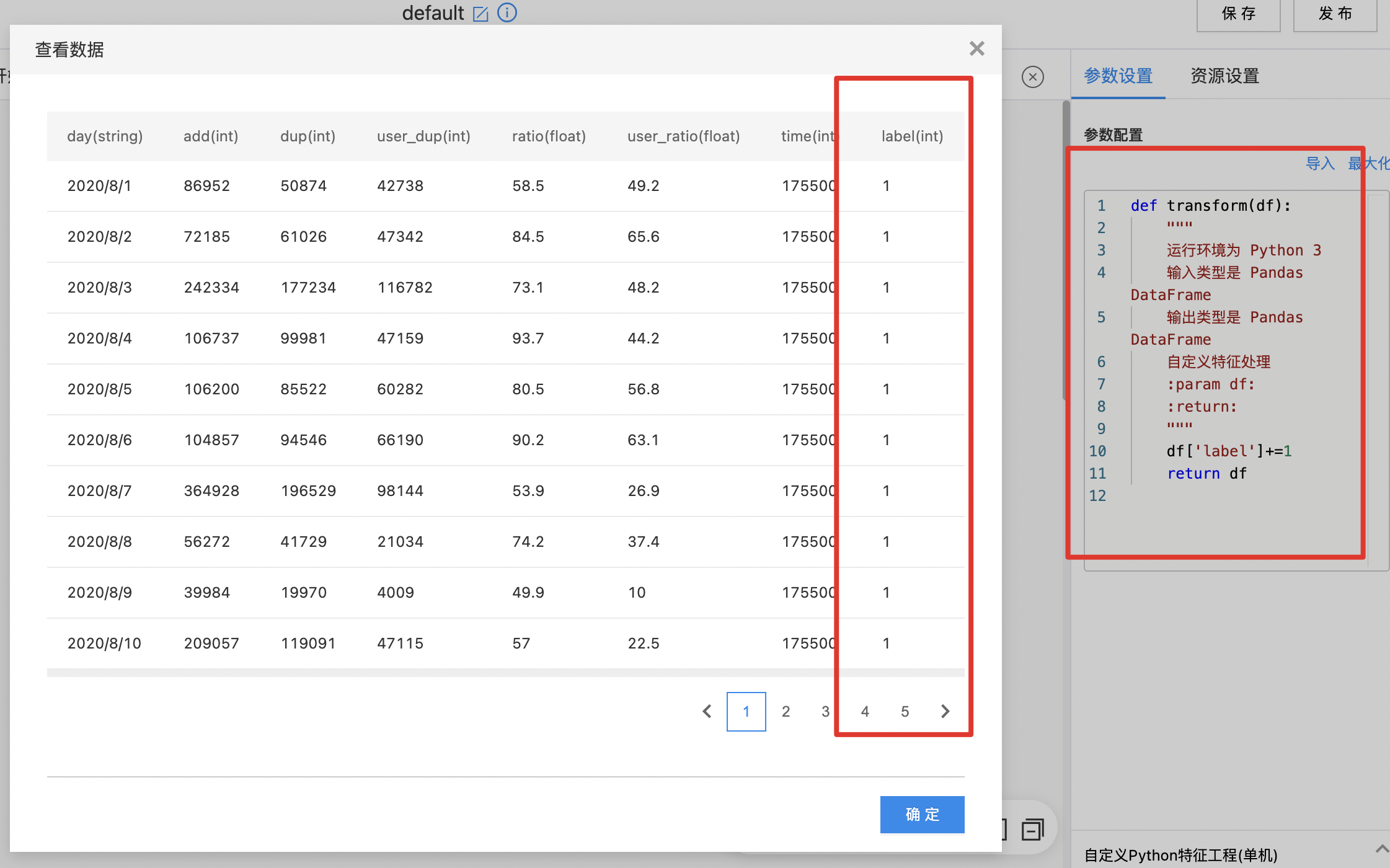
使用示例

1. 拖入数据集组件，选择数据集

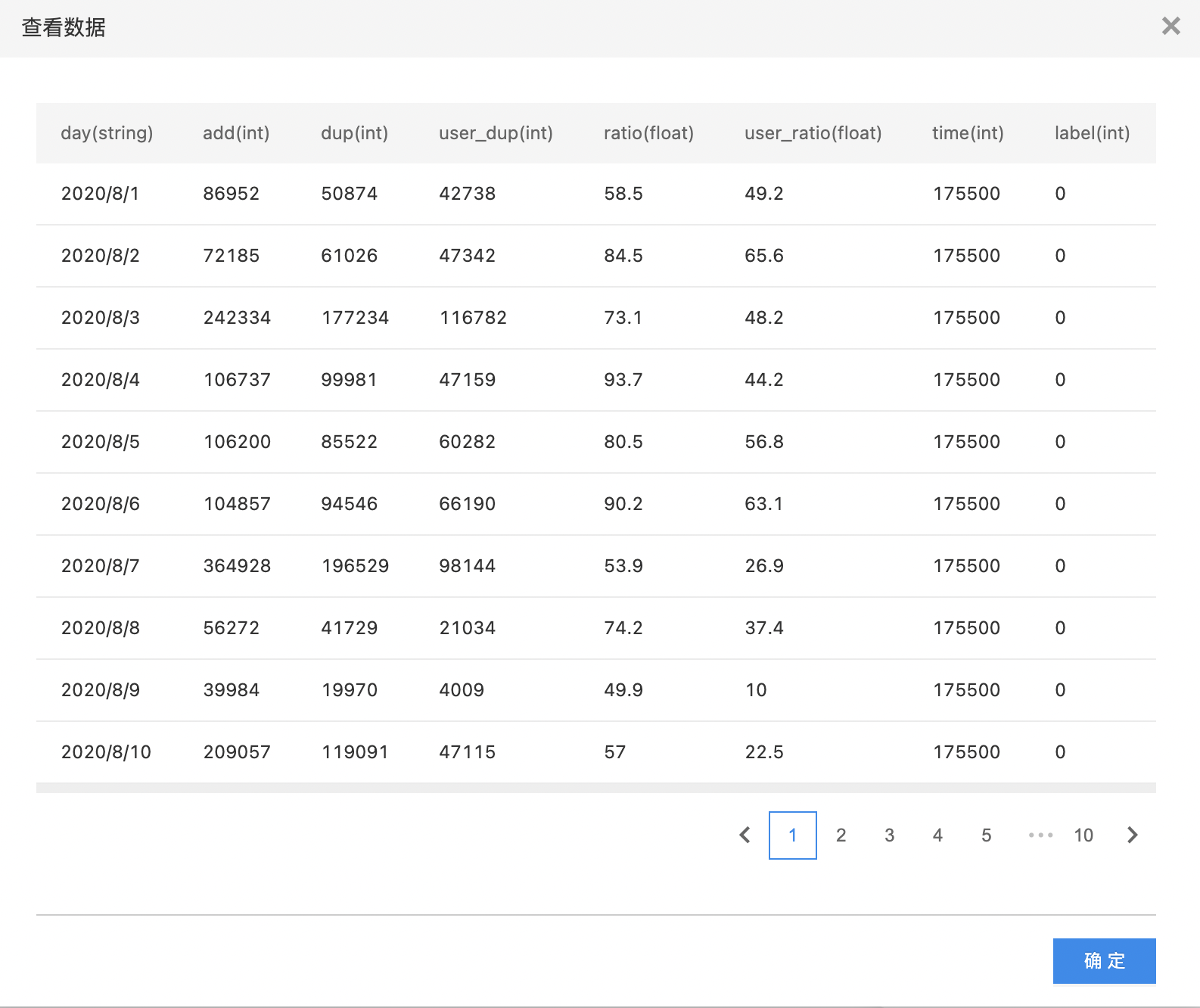
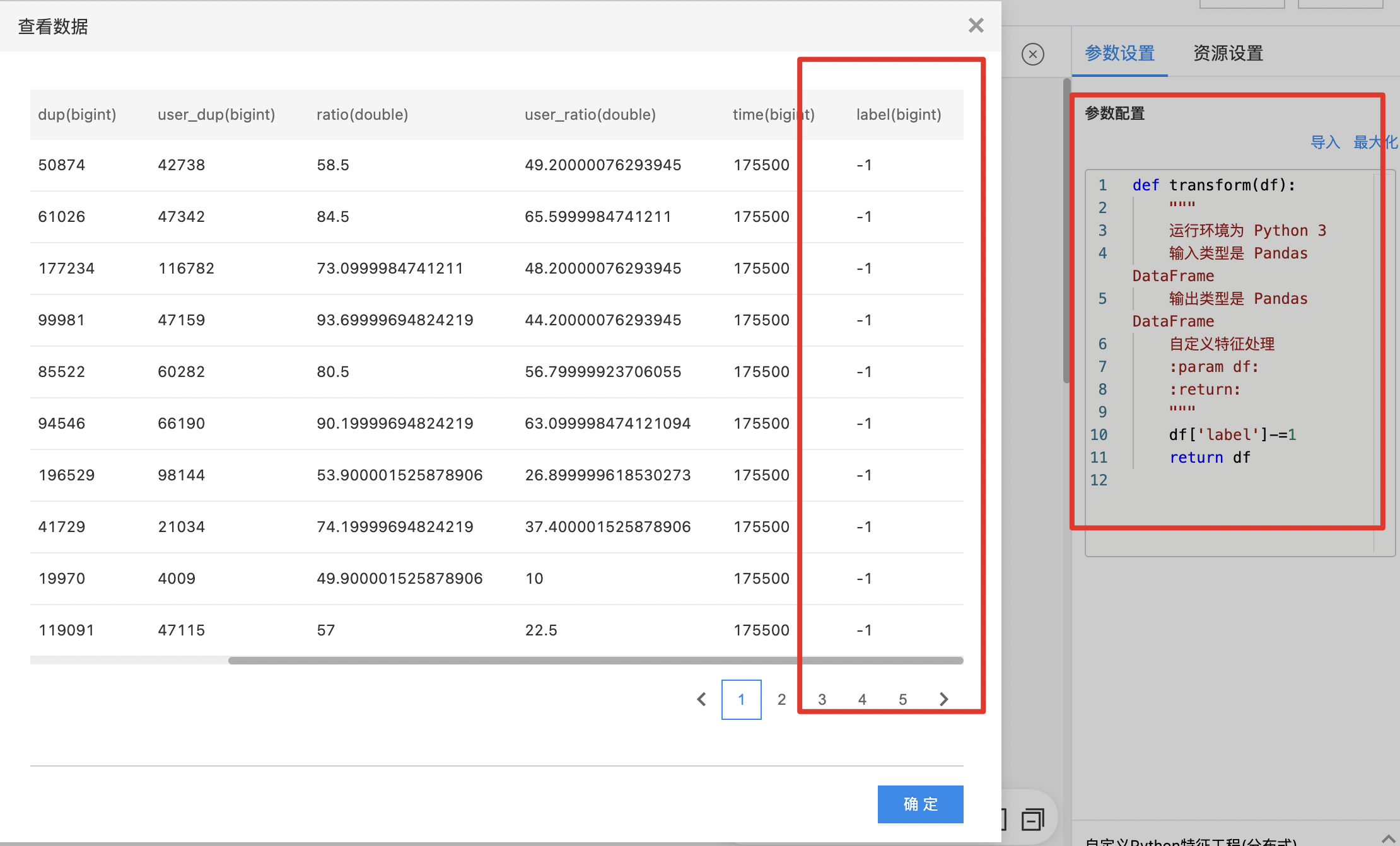
2. 拖入自定义Python特征工程(单机)组件，连接数据集组件后，编写Python代码，运行查看结果

自定义Python特征工程(分布式)

自定义编写Python代码进行特征工程处理，支持多机运行（分布式）。

输入

• 输入一个数据集，需要编写Python代码处理特征。

输出

• 第一个输出是结果数据集。
• 第二个输出是自定义 python 特征工程变换(单机)模型，后续可以使用这个变换操作其它数据集。

算子参数

参数名称	是否必选	参数描述	默认值
Python代码编辑窗口	是	在编辑窗口中编辑数据处理脚本	无

使用示例

1. 拖入数据集组件，选择数据集

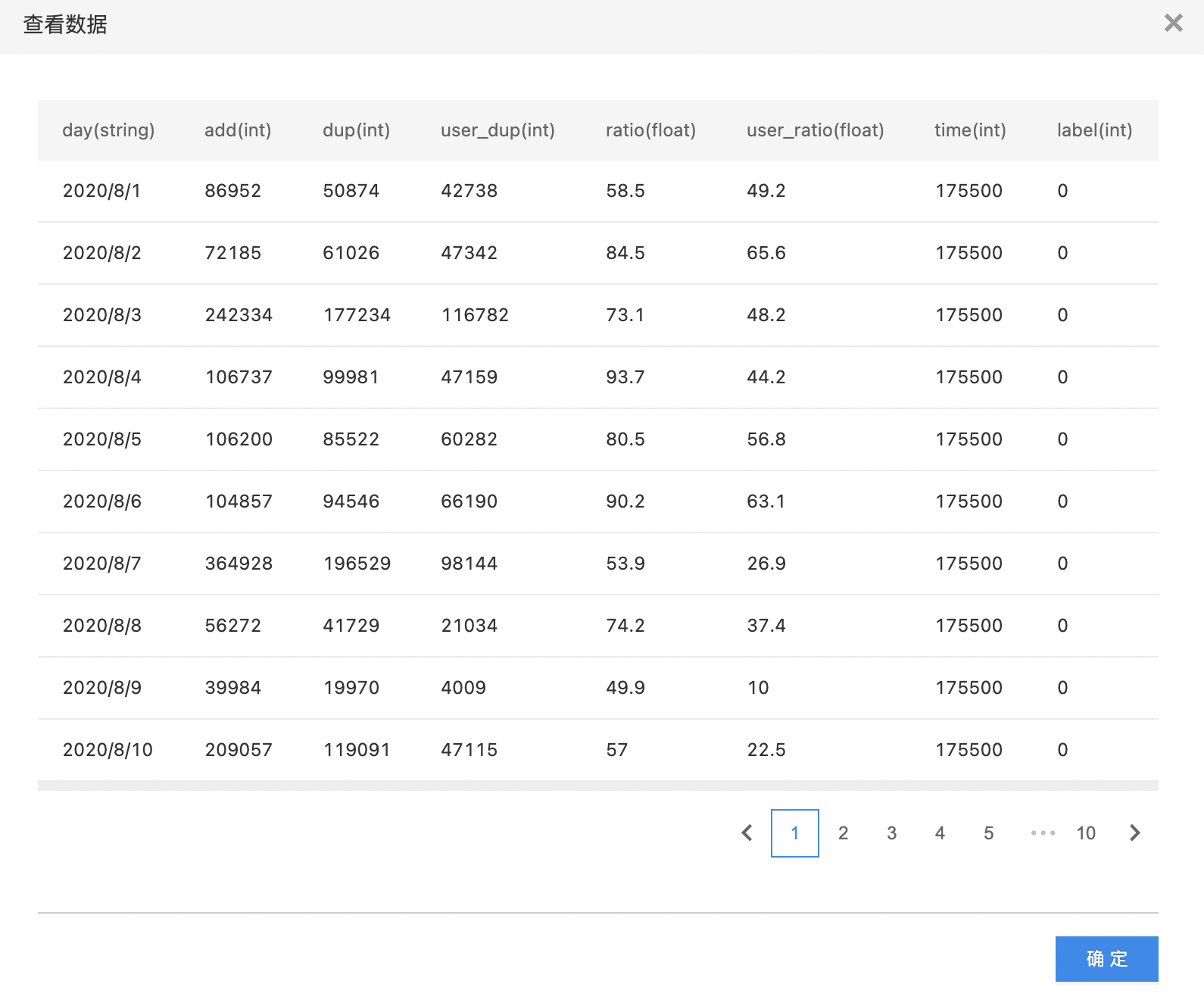
2. 拖入自定义Python特征工程(分布式)组件，连接数据集组件后，编写Python代码，运行查看结果