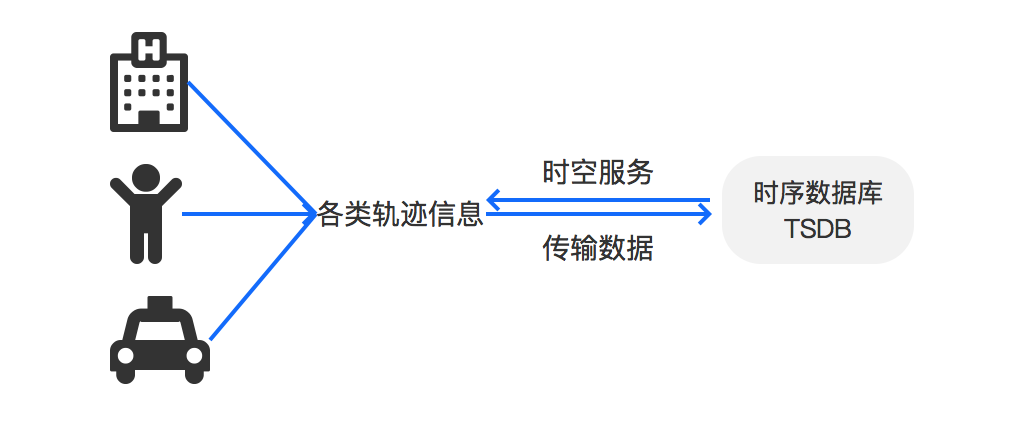
时空服务
TSDB目前已支持时空服务,帮助用户更高效的处理与空间地理位置相关的数据。
使用说明
TSDB目前的SQL查询接口已支持多种与空间地理位置相关的函数,包括二维计算和球面计算。借助这类函数的强大能力,用户可以使用SQL方便地对空间地理位置相关的数据进行计算、分析,挖掘数据价值。
场景一:判断某个设备编号为ABC123的设备是否在某块特定区域内
下图表示TSDB存储的设备位置数据:每个设备的位置信息分别用x_value和y_value两个域(field)来存储,x_value和y_value表示设备在二维坐标系中的坐标;同时用licenseID(Tag)来代表设备号。
可以将这些数据看成一个二维表(如下图),针对此二维表可以通过构造空间函数来使用时空服务。
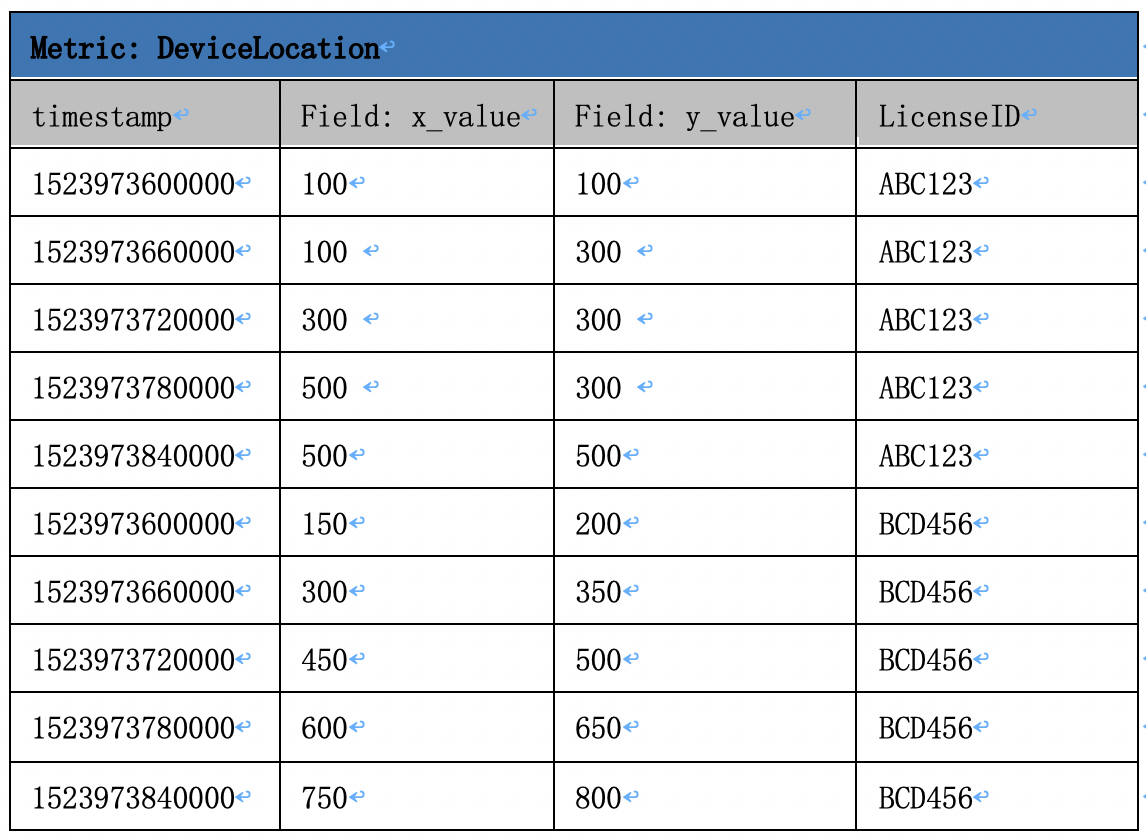
举例: 判断设备ID为ABC123的设备是否在某个特定区域(不包含边界);假定这块区域是由(200, 200), (400, 200), (400, 400),(200, 400)四个点围绕组成的四边形。
SQL语句:
select * from DeviceLocation where ST_Contains(ST_GeometryFromText('POLYGON ((200 200,400 200,400 400,200 400,200 200))'), ST_Point(x_value,y_value)) and LicenseID = ‘ABC123’
返回得到以下数据,证明设备ID为ABC123的设备在时间为1523973720000时在以上指定区域内。

场景二:计算某个车辆在移动的轨迹中,是否经过一块以某个点为中心,一定半径以内的区域
TSDB的时空服务同时支持球面距离的计算,车辆位置和轨迹通常都是通过GPS信息来定位,所以真实的轨迹需要通过球面计算来计算。参考上例,我们可以将上述示例中的x_value和y_value用真实的经度(longitude)和纬度(latitude)来代替表示车辆的实际位置:
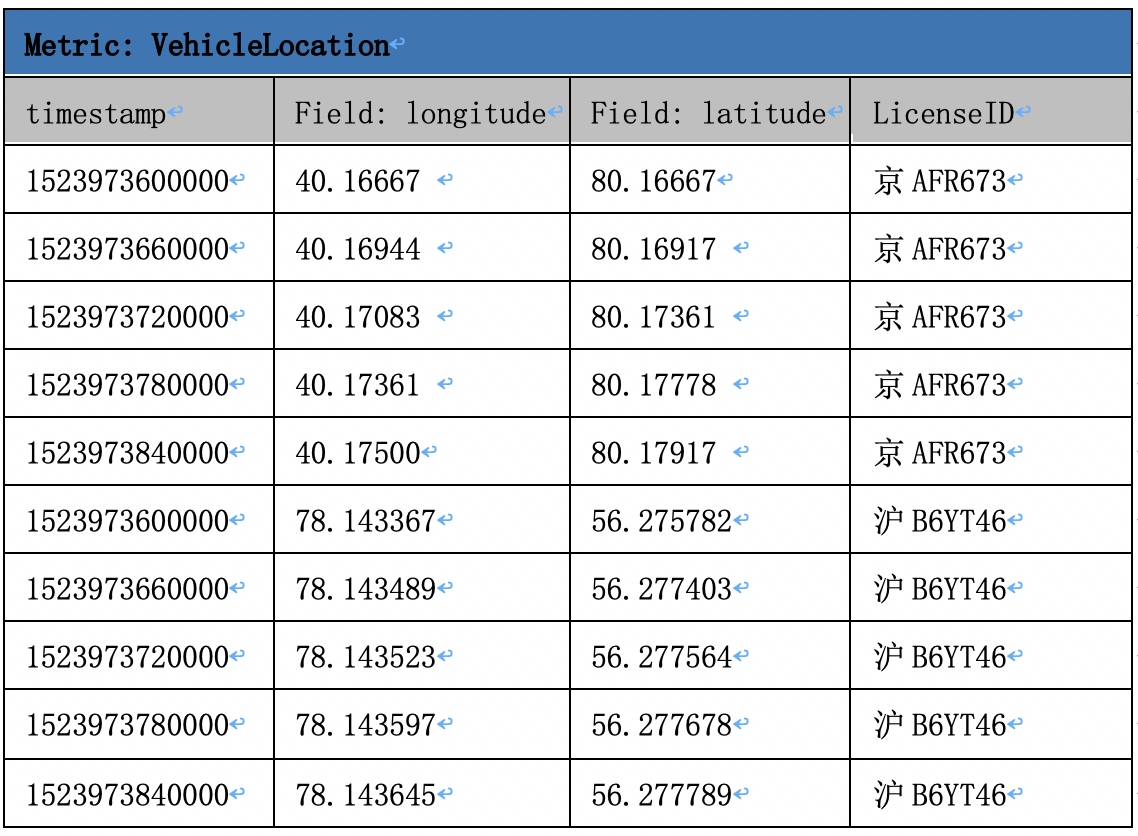
举例: 计算某个车辆在移动的轨迹中,是否经过一块以点(40.17222,80.175)为中心,半径为200m以内的区域。 SQL语句:
select * from VehicleLocation where LicenseID=’京AFR673’and ST_Distance(to_spherical_geography(ST_Point(longitude, latitude)),to_spherical_geography(ST_Point(40.17222, 80.175))) <= 200
返回得到以下数据,证明车牌为京AFR673的车在会时间点为1523973720000时经过以上特定区域。

实际应用
车辆监测
时序数据库用以存储时间、空间数据,借助时空服务,可以实时监测车辆当前行驶路线,在异常情况下,比如车辆脱离既定路线后,能够及时报警;有需要时还能够查看车辆历史行驶轨迹。在检修车作业场景下,判断检修车是否在指定区域内作业;检修车辆的行驶是否偏离预定轨迹;离某个站点最近的救援车是哪一辆等,从而实现车辆的全局优化调控。

轨迹分析
时序数据库用以存储时间、空间数据,借助时空服务,可以计算分析各类轨迹之间的关系,例如分析归纳人流最易聚集的热点区域,特定道路在哪些时间段车辆最多会造成堵塞,在特定区域是否有异常人员、车辆进入。轨迹分析可以应用在非常广泛多样的业务场景中,诸如社区安全、按需选址(如写字楼、医院、商场)、交通分流。
时空服务函数参考
关于SQL语句的使用参考,请参见支持SQL查询。
时空服务构造函数
- ST_Point
声明
1Geometry ST_Point (double X, double Y)作用
根据指定的坐标值(X, Y)返回一个点(Point)类型的几何(Geometry)对象。
示例
1ST_Point(1.0,2.0)返回一个点(Point)类型的几何(Geometry)对象,其横纵坐标分别为1.0和2.0。
- ST_LineFromText
声明
1Geometry ST_LineFromText (varchar WKT)作用
从Well-Known Text (WKT) 的字符串表达式中返回一个线段(LineString)类型的几何(Geometry)对象。
示例
1ST_LineFromText('LINESTRING(1.0 1.5,1.0 0.5)') 返回一个起点为(1.0,1.5),终点为(1.0,0.5)的线段(LineString)类型的几何(Geometry)对象,
- ST_Polygon
声明
Geometry ST_Polygon (varchar WKT)
作用
从Well-Known Text (WKT) 的字符串表达式中返回一个多边形(Polygon)类型的几何(Geometry)对象。
示例
1ST_Polygon('POLYGON ((1 1,1 4,4 4,4 1))') 返回一个由(1,1)、(1,4)、(4,4)、(4,1)四个点组成的多边形(Polygon)类型的几何(Geometry)对象。
- ST_GeometryFromText
声明
1Geometry ST_GeometryFromText (varchar WKT)作用
从Well-Known Text (WKT) 的字符串表达式中返回一个几何(Geometry)对象。
示例
1ST_GeometryFromText('POLYGON ((0 0,1 0,1 1,0 1,0 0))') 返回一个由(0,0)、(0,1)、(1,1)、(1,0)四个点组成的多边形(Polygon)类型的几何(Geometry)对象。
- to_spherical_geography
声明
1SphericalGeography to_spherical_geography (Geometry geometry)作用
把一个几何(Geometry)对象转换为一个球面几何(SphericalGeography)对象。
示例
1to_spherical_geography(ST_Point(40.172, 80.175))返回一个球面几何对象,标识地球上位于东经40.172度,北纬80.175度的点。【-180,0】为西经,【0,180】为东经;【-90,0】为南纬,【0,90】为北纬。
时空服务关系函数
- ST_Contains
声明
1boolean ST_Contains (Geometry A, Geometry B)作用
如果不存在Geometry B中的点落在Geometry A外,且Geometry B内部至少有一个点落在Geometry A内,,返回true,否则返回false。
示例
1ST_Contains(ST_Polygon('POLYGON ((0 0,1 0,1 1,0 1))'), ST_Point(0.5,0.5))=true点(0.5,0.5)完全落在由(0,0)、(0,1)、(1,1)、(1,0)四个点组成的多边形内,所以返回true。
- ST_Equals
声明
1boolean ST_Equals(Geometry A, Geometry B)作用
如果几何(Geometry)对象A和几何(Geometry)对象B代表的是同一个对象,返回true,否则返回false。
示例
1ST_Equals(ST_GeometryFromText('POLYGON ((1 1, 1 3, 3 3, 3 1))'), ST_GeometryFromText('POLYGON ((3 3,3 1,1 1,1 3))')=true由于上述两个多边形完全重合,所以返回true。
- ST_Intersects
声明
1boolean ST_Intersects (Geometry A, Geometry B)作用
如果几何(Geometry)对象A和几何(Geometry)对象B在二维空间上相交,返回true,否则返回false。
示例
1ST_Intersects(ST_GeometryFromText('POLYGON((1 1, 1 3, 3 3, 3 1))'), ST_GeometryFromText('POLYGON ((4 4, 4 5, 5 5, 5 4))'))=false由于这两个矩形没有相交,所以返回false。
- ST_Overlaps
声明
1boolean ST_Overlaps (Geometry A, Geometry B)作用
如果几何(Geometry)对象A和几何(Geometry)对象B有部分重叠,且其中一个并不完全包含另一个,返回true,否则返回false。
示例
1ST_Overlaps(ST_GeometryFromText('POLYGON ((1 1, 1 4, 4 4, 4 1))'), ST_GeometryFromText('LINESTRING (1 1, 4 4)'))=false由于起点为(1,1),终点为(4,4)的线段被完全包含于由(1,1)、(1,4)、(4,4)、(4,1)四个点组成的多边形内,所以即使两者有相交,ST_Overlaps仍返回false。
时空服务访问函数
- ST_Area
声明
1double ST_Area (Geometry A)作用
返回多边形(Polygon)类型的几何(Geometry)对象A二维空间下的面积。
示例
1ST_Area(ST_GeometryFromText('POLYGON ((2 2, 2 6, 6 6, 6 2))'))=16.0返回由(2,2)、(2,6)、(6,6)、(6,2)四个点组成的多边形的面积为16.0。
- ST_Area
声明
1double ST_Area (SphericalGeometry A)作用
返回多边形(Polygon)类型的球面几何(SphericalGeometry)对象A在地球球面上的面积。
示例
1ST_Area(to_spherical_geography(ST_Polygon('POLYGON ((0 0,0 90,90 0))')))=6.375825913974858E13返回由地球球面上的三个点(0,0)、(0,90)、(90,0)组成的多边形的球面面积为6.375825913974858E13平方米。这里地球半径=6371.01千米。
- ST_Distance
声明
1double ST_Distance (Geometry A, Geometry B)作用
返回几何(Geometry)对象A和几何(Geometry)对象B在二维空间下的笛卡尔最短距离。
示例
1ST_Distance(ST_Point(50, 100), ST_Point(150, 150))= 111.80339887498948返回上述两个点(50,100)和(150,150)之间的笛卡尔最短距离为111.80339887498948。
- ST_Distance
声明
1double ST_Distance (SphericalGeometry A, SphericalGeometry B)作用
返回球面几何(SphericalGeometry)对象A和球面几何(SphericalGeometry)对象B在地球球面上的最短距离,单位米。
示例
1ST_Distance(to_spherical_geography(ST_Point(40.175, 80.175)), to_spherical_geography(ST_Point(40.5, 80.5)))= 36643.77019025462返回地球上两个点(40.175, 80.175)和(40.5, 80.5)之间的球面距离为36643.77019025462米。这里地球半径=6371.01千米。
- ST_Length
声明
1double ST_Length (LineString A)作用
返回线段(LineString)类型的几何(Geometry)对象A在二维空间下的长度。
示例
1ST_Length(ST_GeometryFromText('LINESTRING (0 0, 2 2)'))= 2.8284271247461903返回起点为(0,0),终点为(2,2)的线段的长度为2.8284271247461903。
- ST_X
声明
1double ST_X (Point A)作用
返回点(Point)类型的几何(Geometry)对象A的横(X轴)坐标。
示例
1ST_X(ST_GeometryFromText('POINT (1 2)'))=1.0返回点(1,2)的横(X轴)坐标为1.0.
- ST_Y
声明
1double ST_Y (Point A)作用
返回点(Point)类型的几何(Geometry)对象A的纵(Y轴)坐标。
示例
1ST_Y(ST_GeometryFromText('POINT (1 2)'))=2.0返回点(1,2)的纵(Y轴)坐标为2.0.