点距离比优化问题

一键配置（需要提前登陆）

问题背景

点距离比优化问题（Minimizing the Ratio of Maximum to Minimum Distance）源自著名的数学研究网站 Erich's Packing Center，是由数学家 Erich Friedman 提出的一类非凸几何优化难题。当前挑战是在二维空间中放置 16 个点，使得任意两点之间的最大距离与最小距离的比值最小化，追求点集的极致均匀性。

问题介绍

在二维平面上放置n=16 个点，使得： 最小，其中：

• dmax：所有点对之间的最大距离
• dmin：所有点对之间的最小距离

该问题属于非凸空间中的几何优化挑战，由于距离之间高度耦合且函数不具备可微结构，使得常规优化方法容易陷入局部最优，求解过程非常依赖于初始化与策略设计，是衡量优化系统“全局探索能力”的重要基准任务之一。

应用场景

• 无线通信与传感网络布局

  在 5G、物联网（IoT）、雷达系统等场景中，如何布置发射器、基站、传感器等设备的位置，以保障通信覆盖全面、信号均衡且干扰最小，是一项关键任务。

  • 目标与挑战：

    • 避免“盲区”或“重叠干扰区域”
    • 控制设备间最小/最大间距比，保障网络连通性和稳定性

  • 点距离比优化的价值：

    • 使设备间间距分布更均匀，提高网络整体性能和鲁棒性
    • 减少系统对人工调参的依赖，实现自动化部署推荐
• 材料设计与纳米结构排布

在纳米材料、分子结构设计、量子点阵排布等高精度物理场景中，粒子之间的相互作用与排列方式对材料性能（如稳定性、强度、能量状态）影响显著。

1* 目标与挑战：
2    * 平衡粒子间距，避免过密（引发能量过高）或过稀（结构不稳）
3    * 在非凸能量函数下找到稳定排列
4
5* 点距离比优化的价值：
6    * 模拟最优粒子排布策略，辅助材料结构设计
7    * 提供启发式初始解或设计模板，加速材料探索过程

• 高维采样、图生成与建模任务

  在仿真、可视化、3D 建模、GAN 数据生成、图神经网络构图等任务中，均需在空间中生成“分布均匀且信息冗余最小”的点集或连接图。

  • 目标与挑战：

    • 点过密导致冗余，过稀则缺乏表达能力
    • 高维空间中均匀采样极具挑战性

  • 点距离比优化的价值：

    • 提供构建高质量点集的基础算法框架
    • 改善采样多样性与数值稳定性

伐谋成果

伐谋 Agent 在该问题中探索出了一种混合多起点连续优化策略，结合启发式布局初始化与 SLSQP 精确求解算法，实现了全局与局部搜索的协同优化。通过该策略，伐谋 Agent 算得最优比值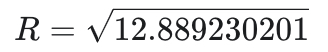，超越 AlphaEvolve 的历史最优纪录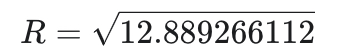，这一成果展现了伐谋 Agent 在数学探索与高维优化中的强大推理与进化能力。

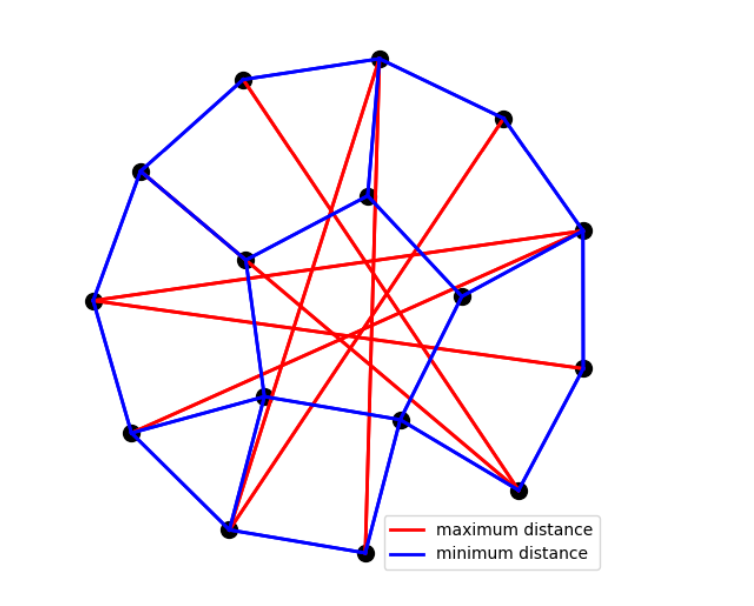
伐谋 Agent 在点距离比优化问题（d=2, n=16）上的结果