如何确定最长无重复数组的长度
作者:文心快码BaiduComate2024.11.07 11:46浏览量:145简介:如何确定最长无重复数组的长度
2024年10月NJSD技术盛典暨第十届NJSD软件开发者大会、第八届IAS互联网架构大会在南京召开。百度文心快码总经理臧志分享了《AI原生研发新范式的实践与思考》,探讨了大模型赋能下的研发变革及如何在公司和行业中落地,AI原生研发新范式的内涵和推动经验。
🔍【大厂面试真题】系列,带你攻克大厂面试真题,秒变offer收割机!
❓今日问题:如何确定最长无重复数组的长度
❤️一起看看文心快码Baidu Comate给出的答案吧!如果这个问题你也会,也可以在评论区写出你的答案哦~

为了达到空间复杂度O(n)和时间复杂度O(nlogn)的要求,我们可以使用滑动窗口结合哈希表(如HashMap或HashSet)来解决这个问题。但通常,使用滑动窗口和哈希表的解法时间复杂度为O(n),空间复杂度为O(n)。如果要严格满足时间复杂度O(nlogn),可能暗示需要使用排序加二分查找等技巧。
这里,我先给出时间复杂度O(n)和空间复杂度O(n)的解法,它是最直观且实用的方法。如果你确实需要O(nlogn)的解法,通常这意味着问题可能转化为其他形式,比如允许对原始数组进行预处理排序。
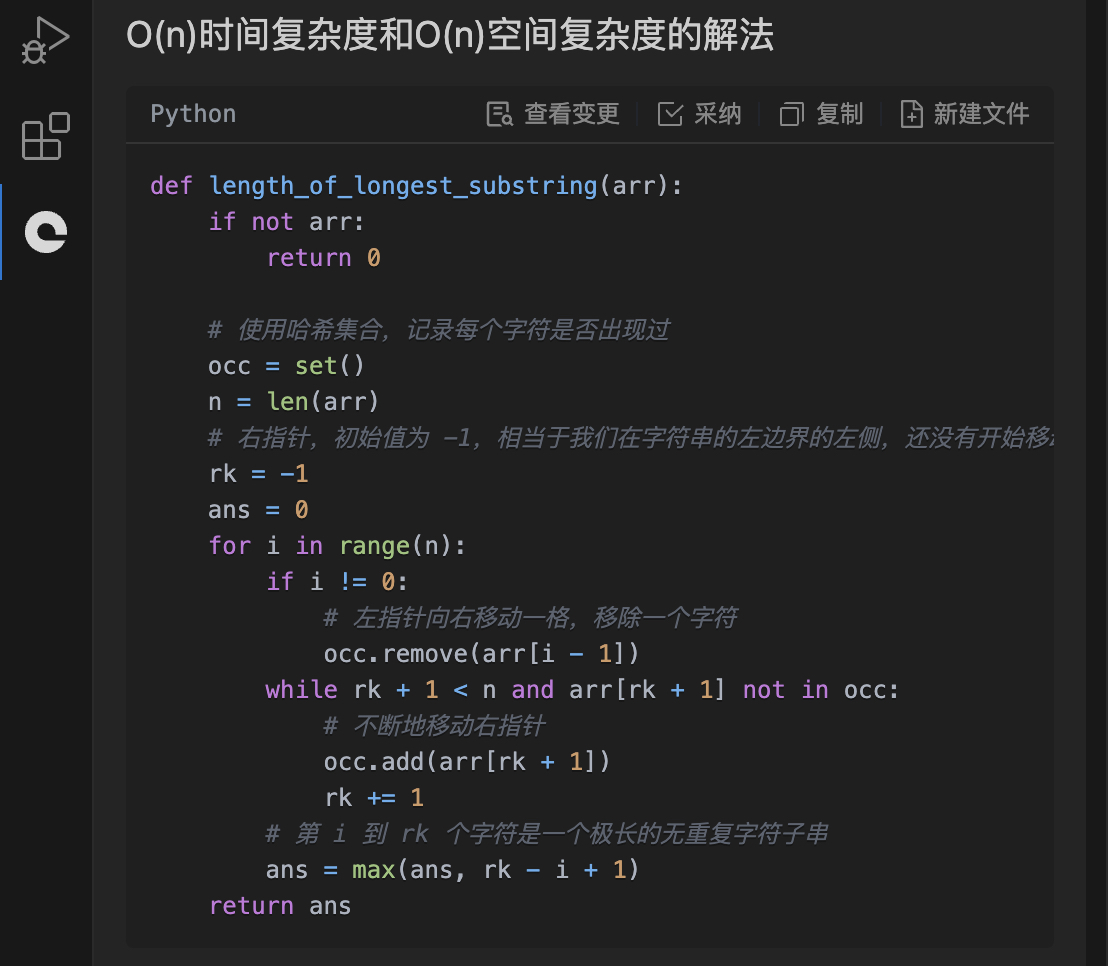
O(n)时间复杂度和O(n)空间复杂度的解法
def length_of_longest_substring(arr):
if not arr:
return 0
# 使用哈希集合,记录每个字符是否出现过
occ = set()
n = len(arr)
# 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动
rk = -1
ans = 0
for i in range(n):
if i != 0:
# 左指针向右移动一格,移除一个字符
occ.remove(arr[i - 1])
while rk + 1 < n and arr[rk + 1] not in occ:
# 不断地移动右指针
occ.add(arr[rk + 1])
rk += 1
# 第 i 到 rk 个字符是一个极长的无重复字符子串
ans = max(ans, rk - i + 1)
return ans
如果你想要一个O(nlogn)时间复杂度的解法,通常涉及到对数组的排序。但排序会改变原数组元素的相对位置,因此这种方法不太适用于直接求解最长无重复子数组问题。然而,如果允许对原问题进行转换,比如先处理一些其他信息(如元素索引),再对它们进行排序,那么有可能构造出一个O(nlogn)的解法。
这里是一个不那么直接但满足O(nlogn)时间复杂度的解法思路:
创建一个辅助数组,其中每个元素包含原始数组中的值和其索引。
根据值对辅助数组进行排序。
使用一个滑动窗口或类似的方法在排序后的数组上处理索引,以跟踪最长无重复子数组的边界。
请注意,这种方法更复杂,可能不如直接的O(n)解法直观或高效。
由于这个问题的直接解法是O(n)的,而且在实际应用中非常有效,因此通常推荐使用。如果你有更具体的要求或上下文,我可以为你提供更详细的O(nlogn)解法示例。
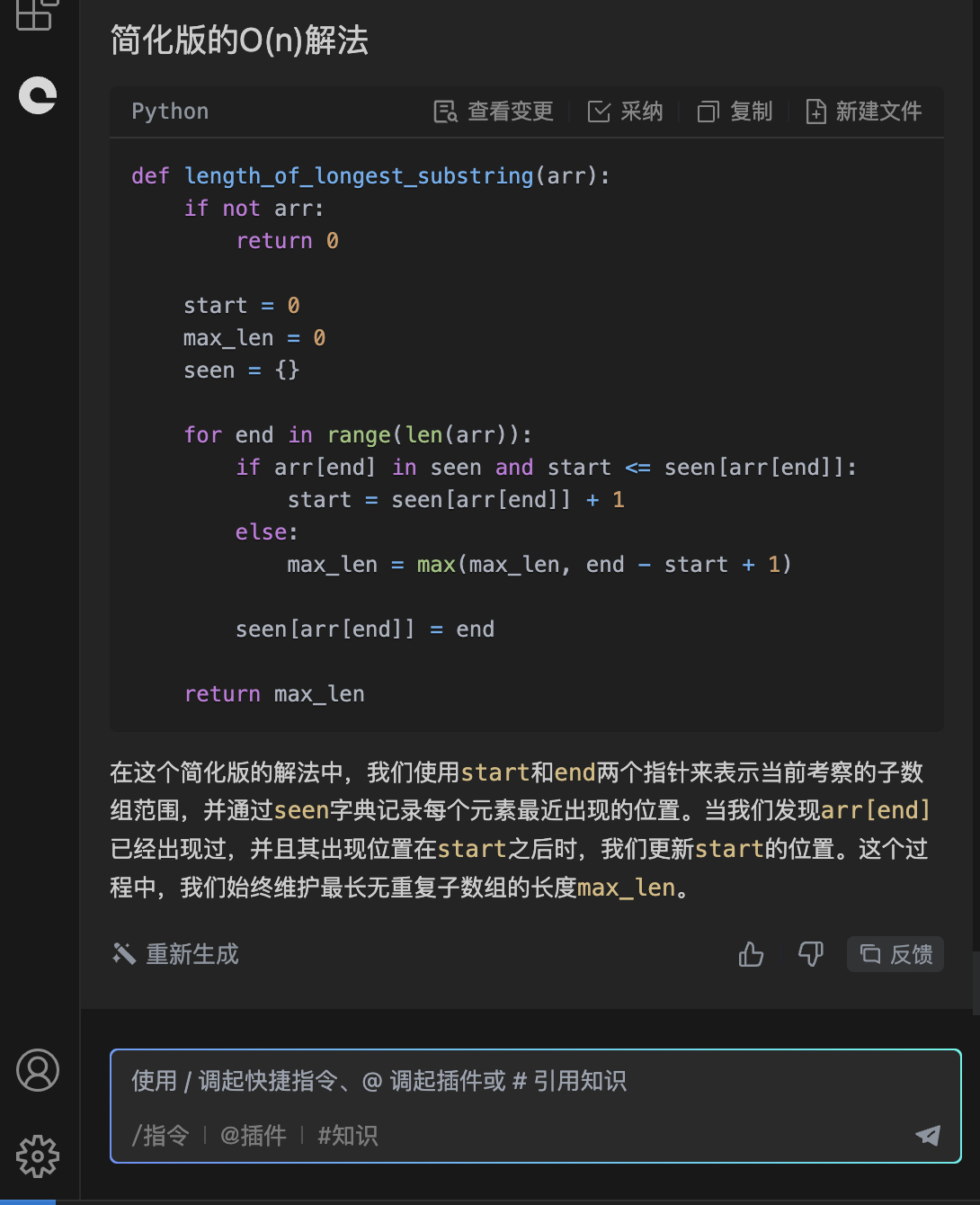
简化版的O(n)解法
def length_of_longest_substring(arr):
if not arr:
return 0
start = 0
max_len = 0
seen = {}
for end in range(len(arr)):
if arr[end] in seen and start <= seen[arr[end]]:
start = seen[arr[end]] + 1
else:
max_len = max(max_len, end - start + 1)
seen[arr[end]] = end
return max_len
在这个简化版的解法中,我们使用start和end两个指针来表示当前考察的子数组范围,并通过seen字典记录每个元素最近出现的位置。当我们发现arr[end]已经出现过,并且其出现位置在start之后时,我们更新start的位置。这个过程中,我们始终维护最长无重复子数组的长度max_len。`