如何进行特征选择?
作者:HelloDeveloper2019.09.24 06:51浏览量:3119简介:很多人说,看了再多的文章,可是没有人手把手地教授,还是很难真正地入门AI。为了将AI知识体系以最简单的方式呈现给你,从这个星期开始,芯君邀请AI专业人士开设“周
很多人说,看了再多的文章,可是没有人手把手地教授,还是很难真正地入门AI。为了将AI知识体系以最简单的方式呈现给你,从这个星期开始,芯君邀请AI专业人士开设“周末学习课堂”——每周就AI学习中的一个重点问题进行深度分析,课程会分为理论篇和代码篇,理论与实操,一个都不能少!
读芯术,一个专注年轻人的AI学习与发展平台(ID:AI_Discovery)。
来,退出让你废寝忘食的游戏页面,取消只有胡吃海塞的周末聚会吧。未来你与同龄人的差异,也许就从每周末的这堂AI课开启了!
全文共2825字,预计学习时长6分钟

大家周末好呀,又见面了。这周我们来说说如何进行特征选择的问题。
一个典型的机器学习任务,是通过样本的特征来预测样本所对应的值。如果样本的特征少了,我们会考虑增加特征,比如Polynomial Regression就是典型的增加特征的算法。在前一周的课程中,相信大家已经体会到,模型特征越多,模型的复杂度也就越高,越容易导致过拟合。事实上,如果我们的样本数少于特征数,那么过拟合就不可避免。
而现实中的情况,往往是特征太多了,需要减少一些特征。
首先是“无关特征”(irrelevant feature)。比如,通过空气的湿度,环境的温度,风力和当地人的男女比例来预测明天会不会下雨,其中男女比例就是典型的无关特征。
其次,要减少的另一类特征叫做“多余特征”(redundant feature),比如,通过房屋的面积,卧室的面积,车库的面积,所在城市的消费水平,所在城市的税收水平等特征来预测房价,那么消费水平(或税收水平)就是多余特征。证据表明,消费水平和税收水平存在相关性,我们只需要其中一个特征就够了,因为另一个能从其中一个推演出来。(如果是线性相关,那么我们在用线性模型做回归的时候,会出现严重的多重共线性问题,将会导致过拟合。)
减少特征有非常重要的现实意义,甚至有人说,这是工业界最重要的问题。因为除了降低过拟合,特征选择还可以使模型获得更好的解释性,加快模型的训练速度,一般的,还会获得更好的性能。
问题在于,在面对未知领域的时候,很难有足够的知识去判断特征与我们的目标是不是相关,特征与特征之间是不是相关。这时候,就需要一些数学和工程上的办法来帮助我们尽可能地把恰好需要的特征选择出来。
常见的方法包括过滤法(Filter)、包裹法(Warpper),嵌入法(Embedding)。接下来,我们对每一种方法分举一例,来说明每种方法对应的特征选择如何进行的。
过滤(Filter)
过滤法只用于检验特征向量和目标(响应变量)的相关度,不需要任何的机器学习的算法,不依赖于任何模型,只是应用统计量做筛选:我们根据统计量的大小,设置合适的阈值,将低于阈值的特征剔除。
所以,从某种程度上来说,过滤法更像是一个数学问题,我们只在过滤之后的特征子集上进行建模和训练。
相关系数(Correlation coefficient)
我们都知道,随机变量的方差度量的是变量的变异程度,而两个随机变量的协方差(Covariance)度量的是它们联合变异程度。如果X、Y是分别具有期望 ,
, 的随机变量,那么它们的协方差定义为
的随机变量,那么它们的协方差定义为 。可以看出,协方差就是X与其均值偏离程度和Y与其均值偏离程度的乘积平均值。
。可以看出,协方差就是X与其均值偏离程度和Y与其均值偏离程度的乘积平均值。
也就是说,如果X大于其均值,Y也倾向于大于其均值,那么协方差就为正,表明关联是正向的,如果X大于其均值,Y倾向于小于其均值,那么协方差就为负,表明关联是负向的。我们可以将其展开:
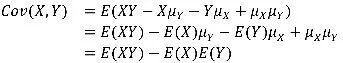
如果X和Y相互独立,那么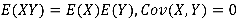 。(反之不一定成立)
。(反之不一定成立)
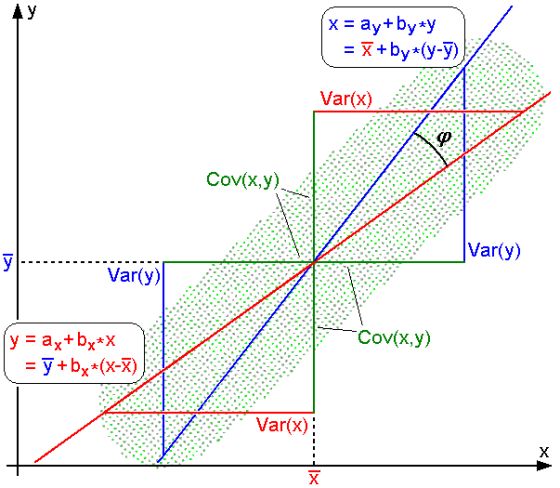
图为 和
和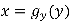 的示意图,其中方差
的示意图,其中方差 刻画了随机变量偏离均值的程度,
刻画了随机变量偏离均值的程度,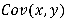 刻画了两者的线性相关程度,可以直观的看出,两条线的夹角越大,则x,y的相关性越大,那么
刻画了两者的线性相关程度,可以直观的看出,两条线的夹角越大,则x,y的相关性越大,那么 越大。
越大。
一个自然的想法是,能否将角度作为衡量两个随机变量的指标呢?事实上,我们在此基础上定义相关系数:

对应的正是 。相关系数不仅在几何上更为直观,而且将相关度的测量无量纲化,相关度就不再依赖于测量单位。
。相关系数不仅在几何上更为直观,而且将相关度的测量无量纲化,相关度就不再依赖于测量单位。

图为理想情况下,挑选的特征空间对应的相关系数。
包裹(Warpper)
与过滤法不同的是,包裹法采用的是特征搜索的办法。它的基本思路是,从初始特征集合中不断的选择子集合,根据学习器的性能来对子集进行评价,直到选择出最佳的子集。在搜索过程中,我们会对每个子集做建模和训练。

图为包裹法的流程图,其中Estimated Accuracy是机器学习分类问题的典型的性能指标。
基于此,包裹法很大程度上变成了一个计算机问题:在特征子集的搜索问题(subset search)。我们有多种思路,最容易想到的办法是穷举(Brute-force search),遍历所有可能的子集,但这样的方法适用于特征数较少的情形,特征一旦增多,就会遇到组合爆炸,在计算上并不可行。(N个特征,则子集会有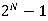 种可能)
种可能)
另一个思路是随机化搜索,比如拉斯维加斯算法(Las Vegas algorithm),但这样的算法在特征数大的时候,计算开销仍然很大,而且有给不出任何解的风险。所以,我们常使用的是贪心算法:
- 前向搜索(Forward search)
在开始时,按照特征数来划分子集,每个子集只有一个特征,对每个子集进行评价。然后在最优的子集上逐步增加特征,使模型性能提升最大,直到增加特征并不能使模型性能提升为止。
- 后向搜索(Backward search)
在开始时,将特征集合分别减去一个特征作为子集,每个子集有N—1个特征,对每个子集进行评价。然后在最优的子集上逐步减少特征,使得模型性能提升最大,直到减少特征并不能使模型性能提升为止。
- 双向搜索(Bidirectional search)
将Forward search 和Backward search结合起来。
- 递归剔除(Recursive elimination )
反复的训练模型,并剔除每次的最优或者最差的特征,将剔除完毕的特征集进入下一轮训练,直到所有的特征被剔除,被剔除的顺序度量了特征的重要程度。
嵌入法(Embedding)
如果仔细思考前两种方法,过滤法与学习器没有关系,特征选择只是用统计量做筛选,而包裹法则固定了学习器,特征选择只是在特征空间上进行搜索。而嵌入法最大的突破在于,特征选择会在学习器的训练过程中自动完成。
如果你还记得降低过拟合的理论,那么一定记得Ridge Regression和LASSO:

它们实际上并没有改变本身的模型,只是在优化函数(均方误差)的基础上添加参数的范数,参数 的大小反映了正则项与均方误差的相对重要性,
的大小反映了正则项与均方误差的相对重要性,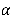 越大,正则项的权重就会越大,优化参数的结果就会偏好更小的参数值。
越大,正则项的权重就会越大,优化参数的结果就会偏好更小的参数值。
事实上,它们是通过降低权重系数的办法来降低过拟合,那么在线性模型中,降低权重系数就意味着与之相关的特征并不重要,实际上就是对特征做了一定的筛选。
其中LASSO的方法可以将某些权重系数降为零,这意味着,只有权重系数不为零的特征才会出现在模型中。换言之,基于正则化的方法就是一种标准的嵌入法。
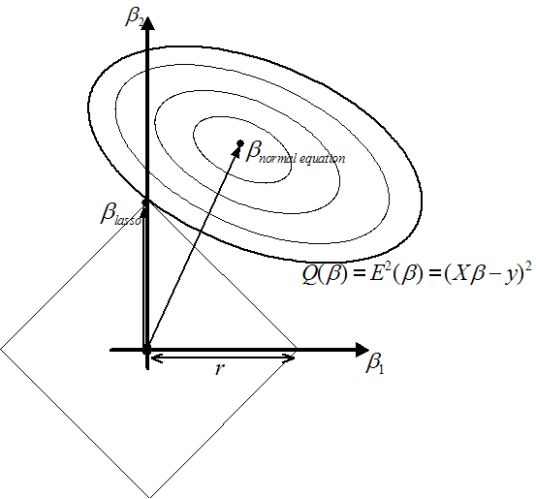
图为LASSO优化结果示意,均方误差项加了正则项的效果就是:整体的优化结果不会迭代到黑点(终点),而是迭代到它们的交点,而且交点往往在轴上。
除此之外,决策树也是典型的嵌入法。因为决策树是利用一个特征进行分类,我们在生成决策树的过程就是挑选特征的过程,并且根据特征的不同取值构建子节点,直到特征没有分类能力或者很小,就停止生成节点。
读芯君开扒
课堂TIPS
- 本文所说的相关系数又叫做Pearson相关系数,实际上,Pearson相关系数能被看作夹角余弦值的重要前提是数据的中心化,而中心化的思想来源于高斯分布。所以Pearson相关系数更多的是测量服从正态分布的随机变量的相关性,如果这个假设并不存在,那么可以使用spearman相关系数。
- 过滤法应用于回归问题,还可以采用互信息法(Mutual Information ),应用分类问题则可以使用卡方检验(Chi-Squared Test )。
- 我们将多个决策树集成起来,会获得随机森林(Random Forests ),与决策树一样,它可以在决定类别时,评估特征的重要性,从而实现特征选择的作用.xgboost也会起到类似的作用。
- 深度学习具有自动学习特征的能力,而特征选择是机器学习非常重要的一环,这也是深度学习能取得重大成功的原因之一。